diff --git a/.github/workflows/CompatHelper.yml b/.github/workflows/CompatHelper.yml
new file mode 100644
index 0000000..9ef7b5a
--- /dev/null
+++ b/.github/workflows/CompatHelper.yml
@@ -0,0 +1,27 @@
+name: CompatHelper
+
+on:
+ schedule:
+ - cron: '00 * * * *'
+ issues:
+ types: [opened, reopened]
+
+jobs:
+ build:
+ runs-on: ${{ matrix.os }}
+ strategy:
+ matrix:
+ julia-version: [1.3.1]
+ julia-arch: [x86]
+ os: [ubuntu-latest]
+ steps:
+ - uses: julia-actions/setup-julia@latest
+ with:
+ version: ${{ matrix.julia-version }}
+ - name: Install dependencies
+ run: julia -e 'using Pkg; Pkg.add(Pkg.PackageSpec(name = "CompatHelper", url = "https://github.com/bcbi/CompatHelper.jl.git"))'
+ - name: CompatHelper.main
+ env:
+ GITHUB_TOKEN: ${{ secrets.GITHUB_TOKEN }}
+ JULIA_DEBUG: CompatHelper
+ run: julia -e 'using CompatHelper; CompatHelper.main()'
diff --git a/.gitmodules b/.gitmodules
new file mode 100644
index 0000000..a2011b9
--- /dev/null
+++ b/.gitmodules
@@ -0,0 +1,3 @@
+[submodule "benchmark-results"]
+ path = benchmark-results
+ url = C:/Users/yahyaaba/Documents/GitHub/AcuteBenchmark-Results
diff --git a/README.md b/README.md
index 385f060..390cf62 100644
--- a/README.md
+++ b/README.md
@@ -3,7 +3,7 @@
[](https://ci.appveyor.com/project/Crown421/IntelVectorMath-jl)
This package provides bindings to the Intel MKL [Vector Mathematics Functions](https://software.intel.com/en-us/node/521751).
-This is often substantially faster than broadcasting Julia's built-in functions, especially when applying a transcendental function over a large array.
+This is often substantially faster than broadcasting Julia's built-in functions, especially when applying a transcendental function over a large array.
Until Julia 0.6 the package was registered as `VML.jl`.
## Basic install
@@ -24,8 +24,8 @@ julia> ] add https://github.com/JuliaMath/IntelVectorMath.jl
## Using IntelVectorMath
After loading `IntelVectorMath`, you have the supported function listed below, for example `IntelVectorMath.sin(rand(100))`. These should provide a significant speed-up over broadcasting the Base functions.
-Since the package name is quite long, an alias `IVM` is also exported to allow `IVM.sin(rand(100))` after `using` the package.
-If you `import` the package, you can add this alias via `const IVM = IntelVectorMath`. Equally, you can replace `IVM` with another alias of your choice.
+Since the package name is quite long, an alias `IVM` is also exported to allow `IVM.sin(rand(100))` after `using` the package.
+If you `import` the package, you can add this alias via `const IVM = IntelVectorMath`. Equally, you can replace `IVM` with another alias of your choice.
#### Example
```julia
@@ -87,16 +87,87 @@ regarding these options is available on
[Intel's website](http://software.intel.com/sites/products/documentation/hpc/mkl/IntelVectorMath/vmldata.htm).
## Performance
-(These results are currently outdated and will be updated in due course)
-
-
-
-
-Tests were performed on an Intel(R) Core(TM) i7-3930K CPU. Error bars
-are 95% confidence intervals based on 25 repetitions of each test with
-a 1,000,000 element vector. The dashed line indicates equivalent
-performance for IntelVectorMath versus the implementations in Base. Both Base and
-IntelVectorMath use only a single core when performing these benchmarks.
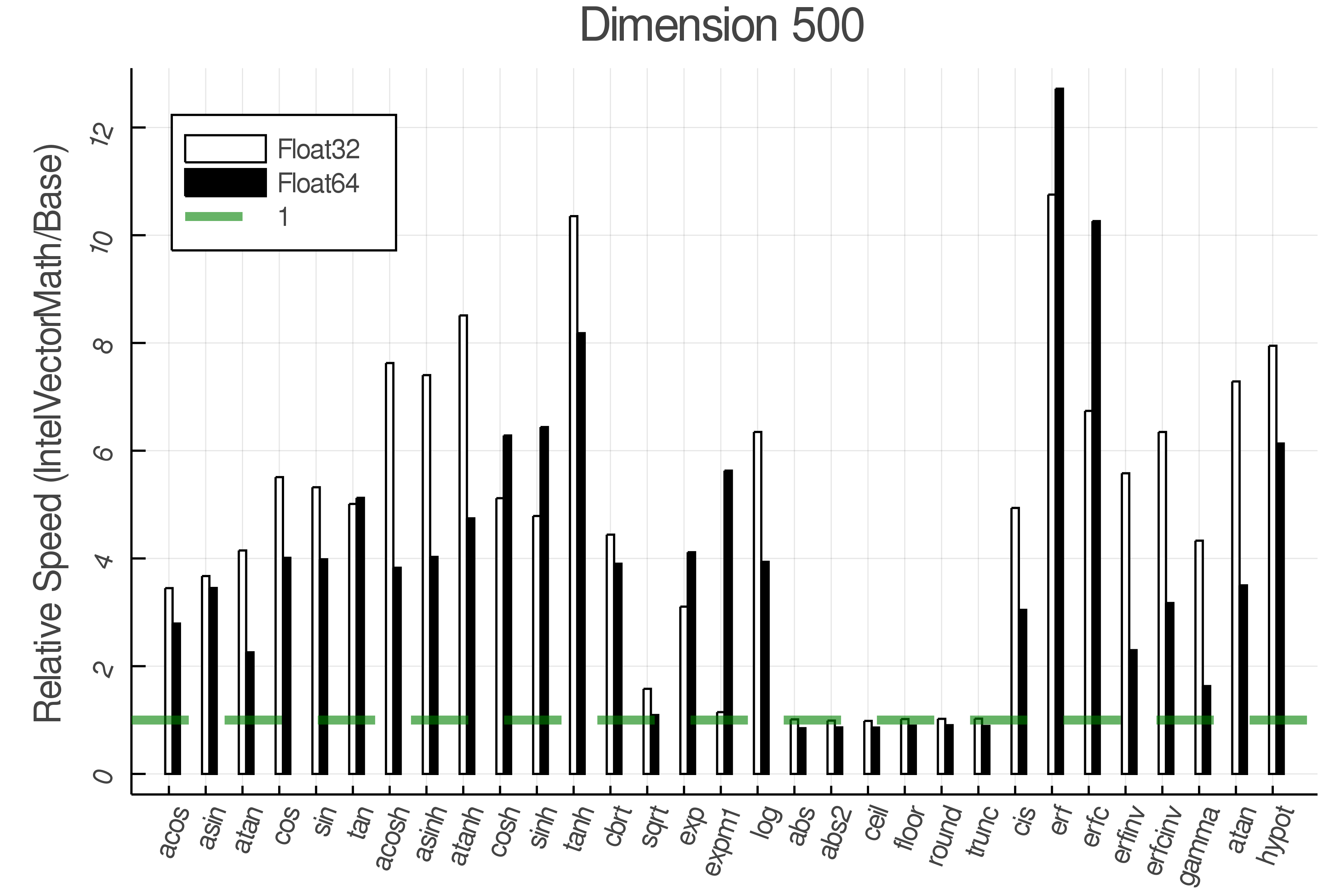
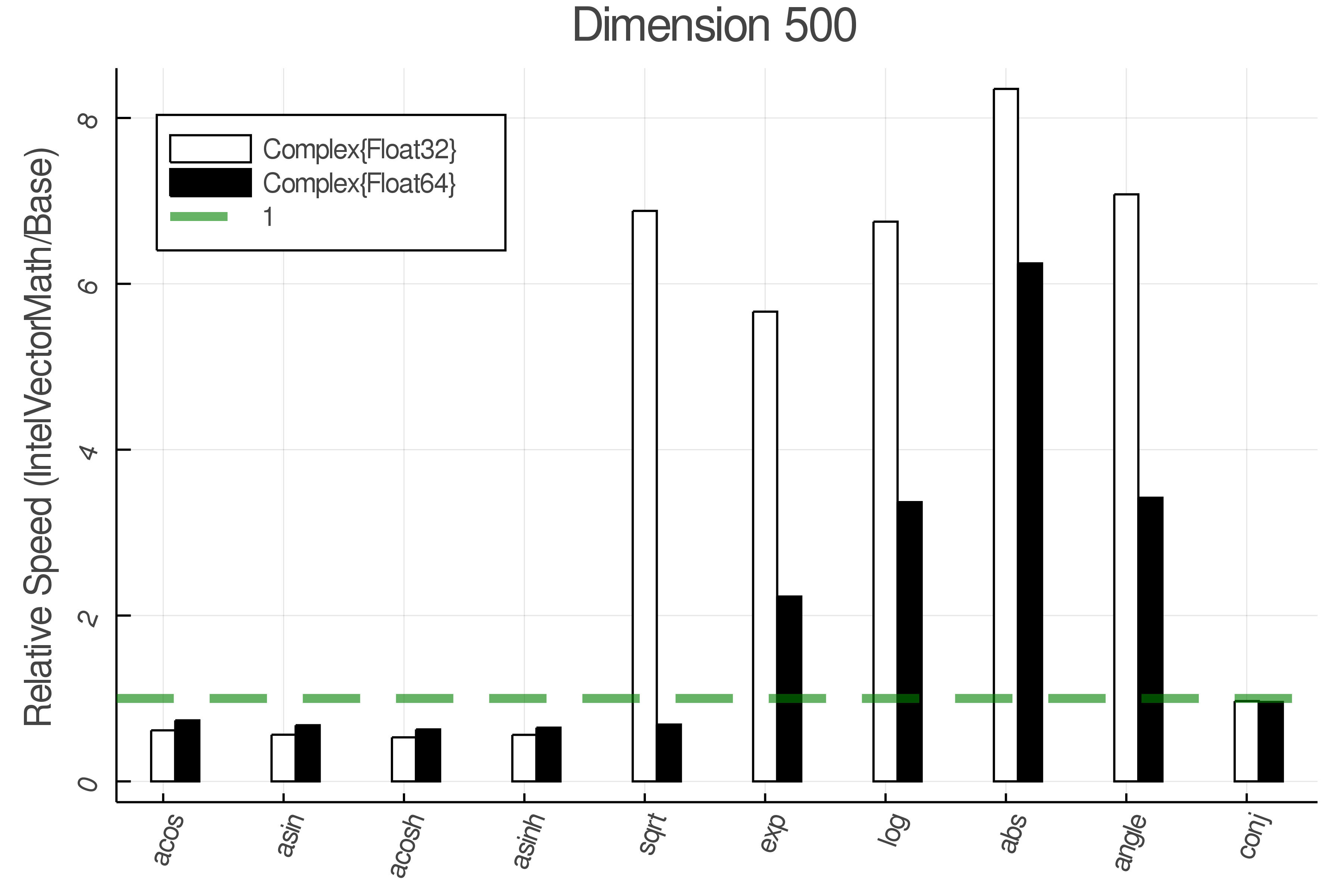
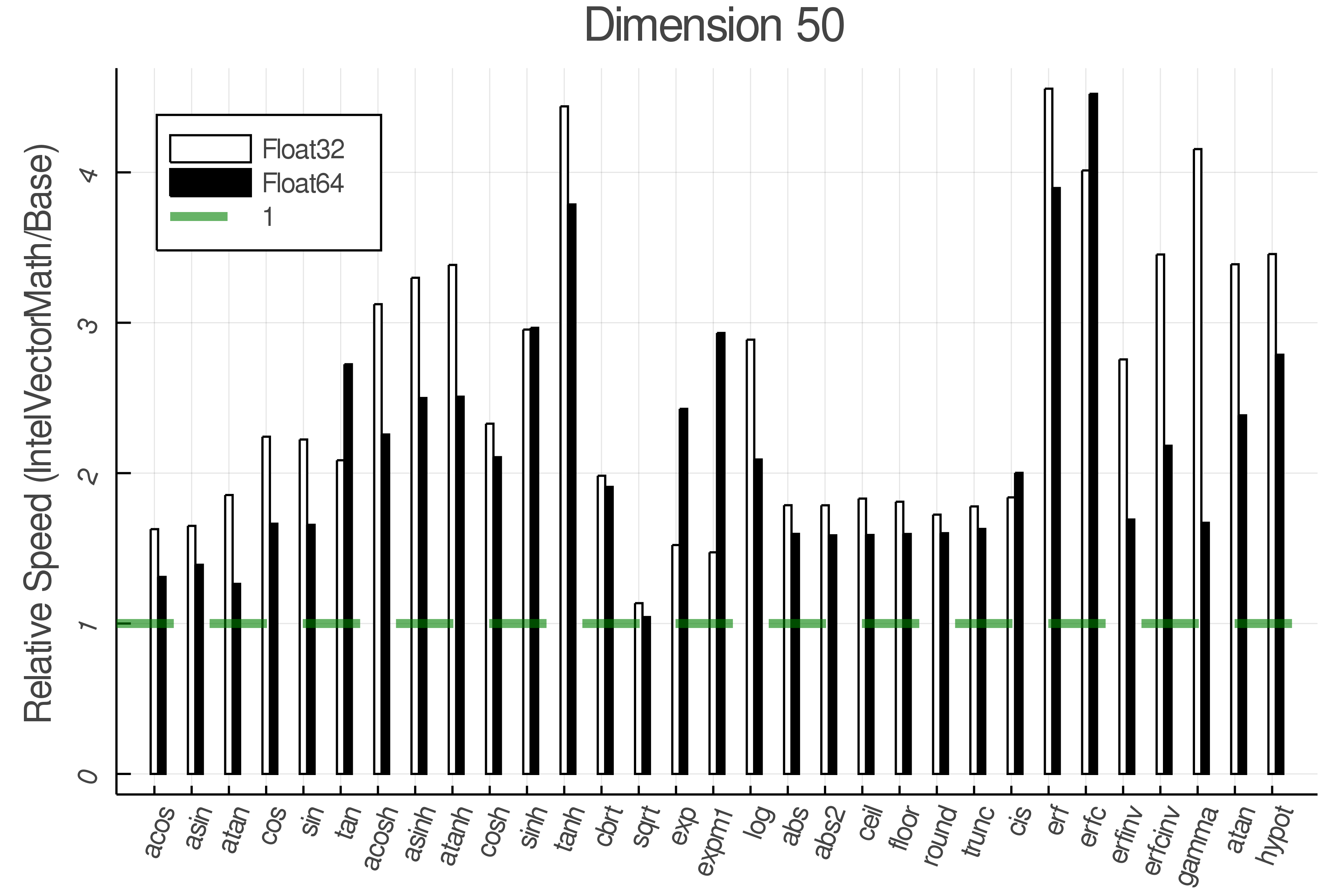
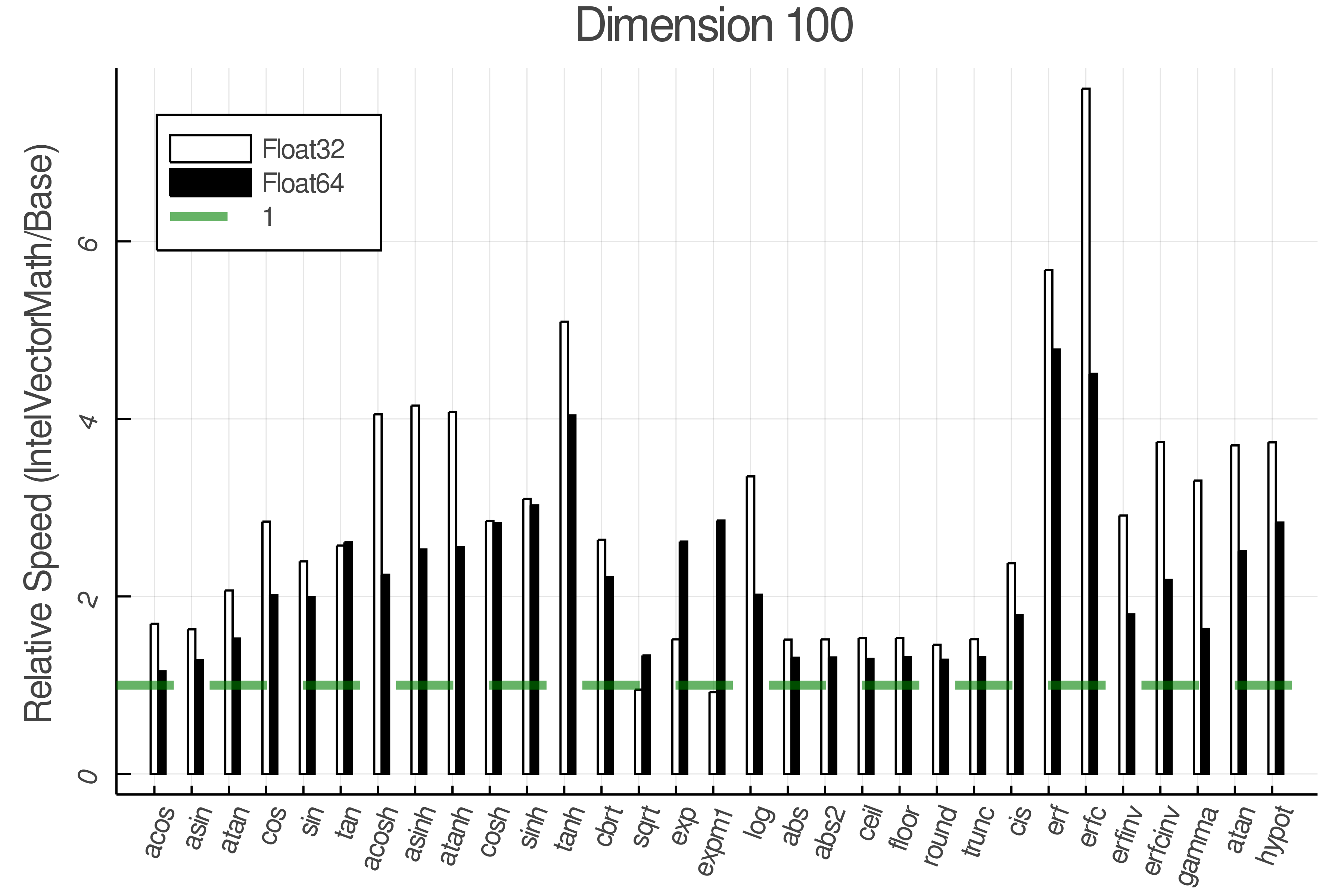
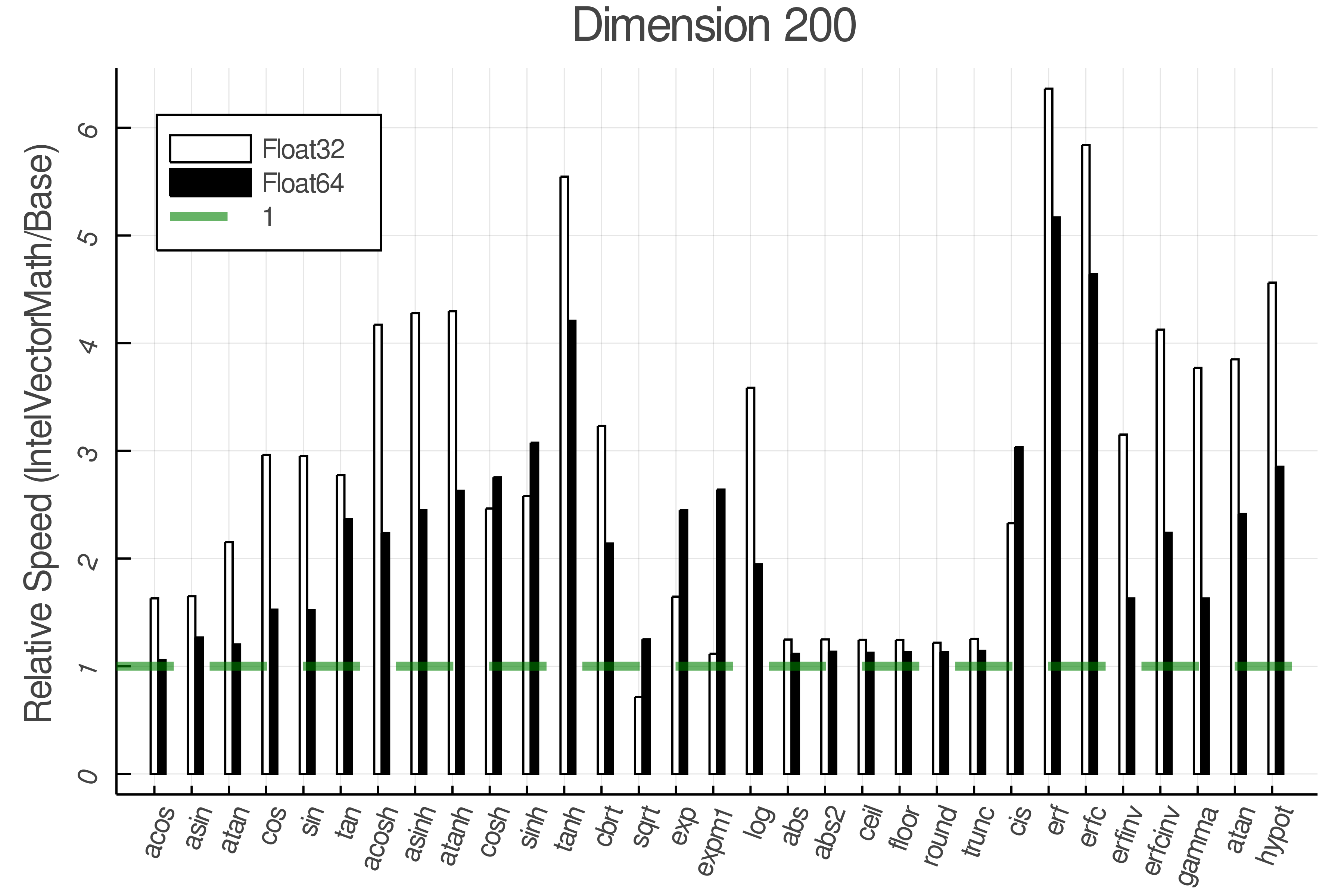
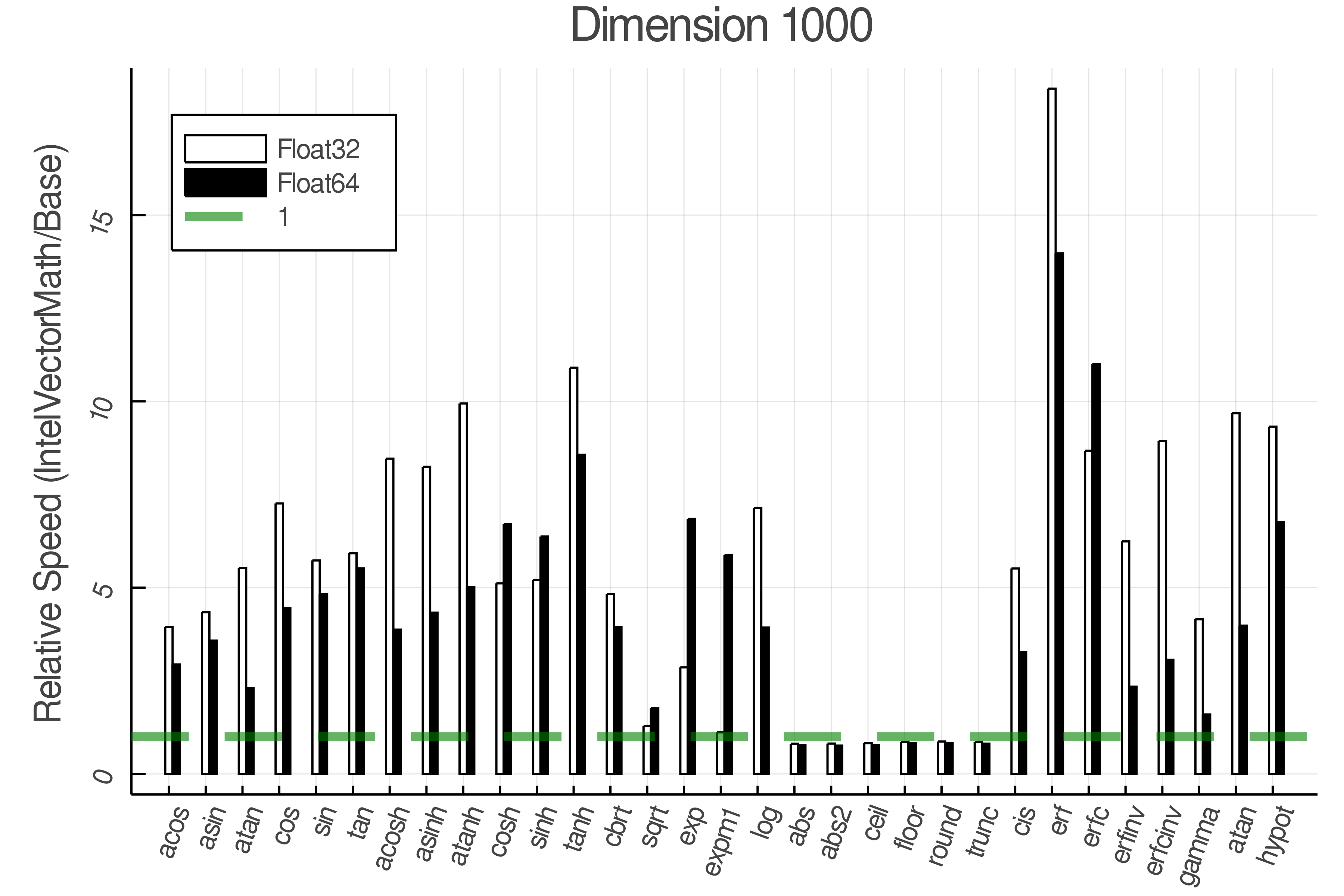
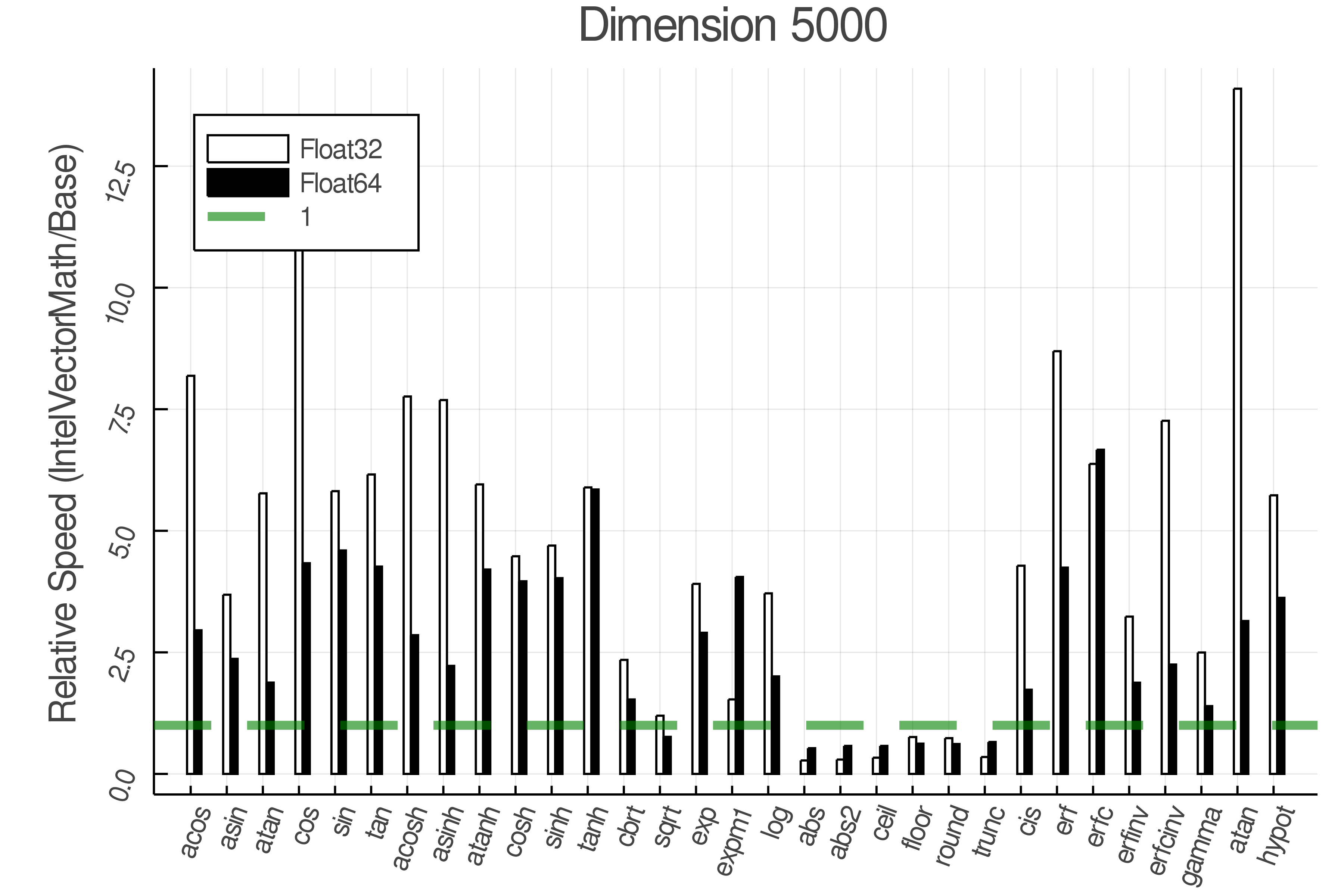
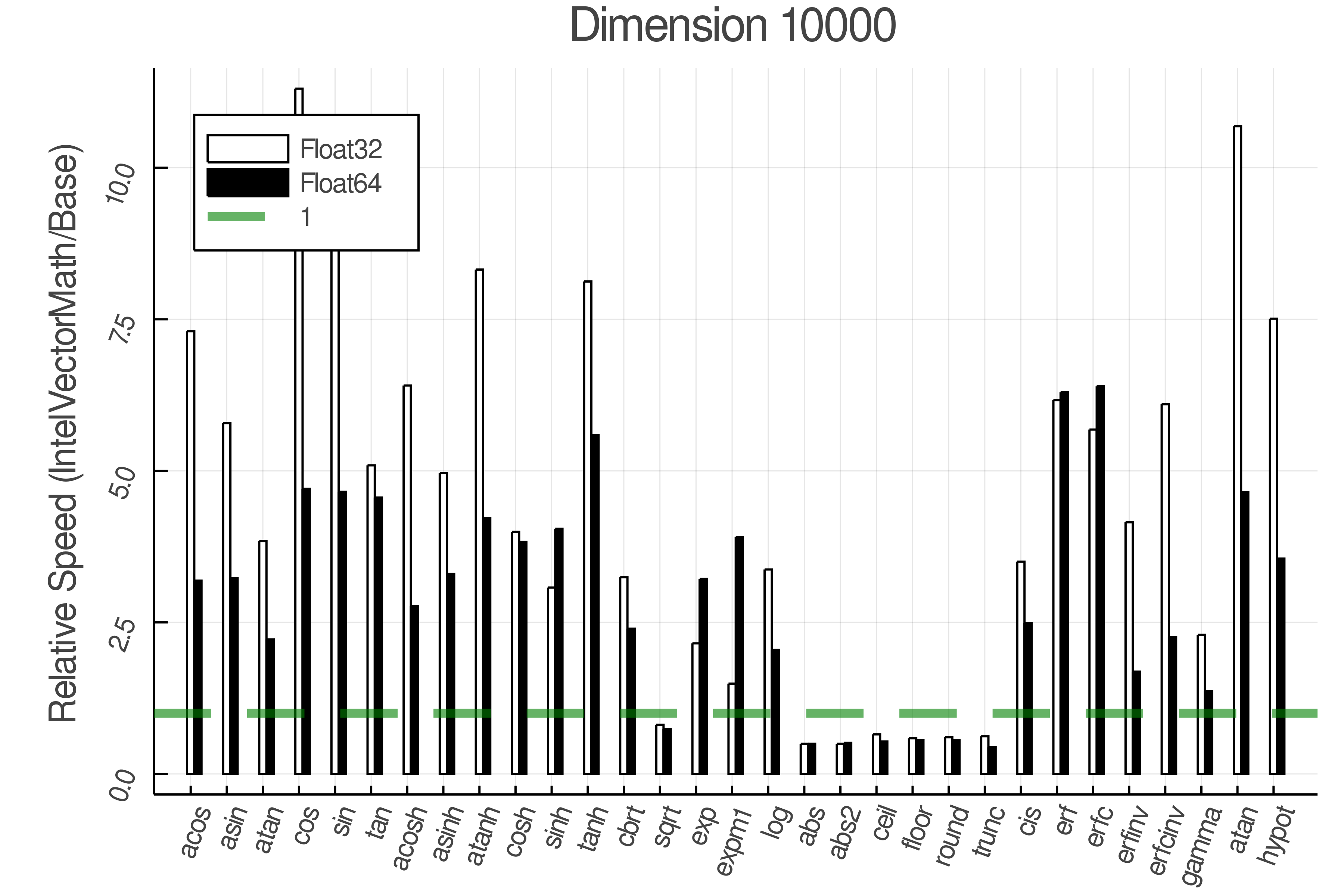
+Summary of Results:
+
+Relative speed of IntelVectorMath/Base
+
+
+
+
+
+Full Results:
+
+
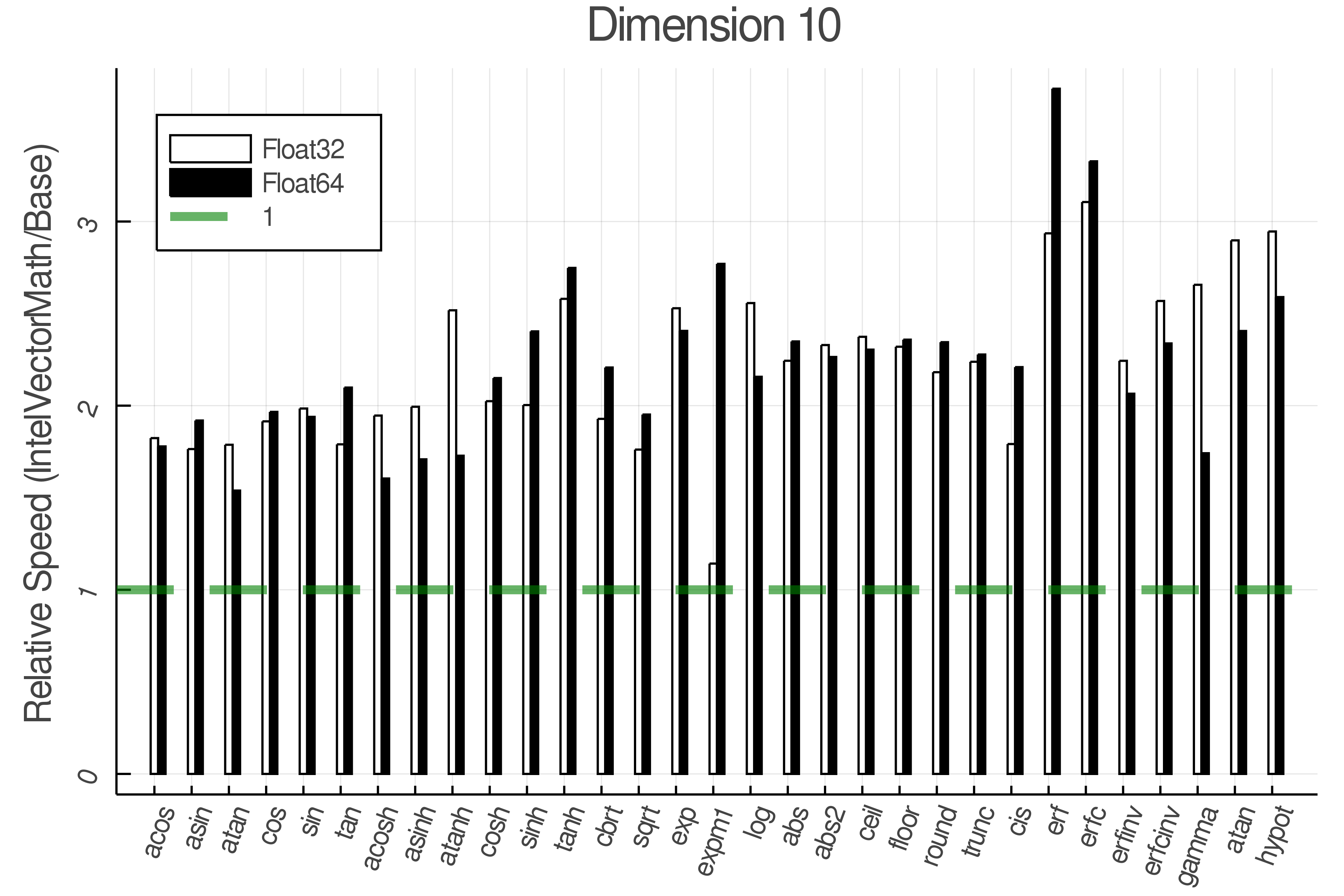
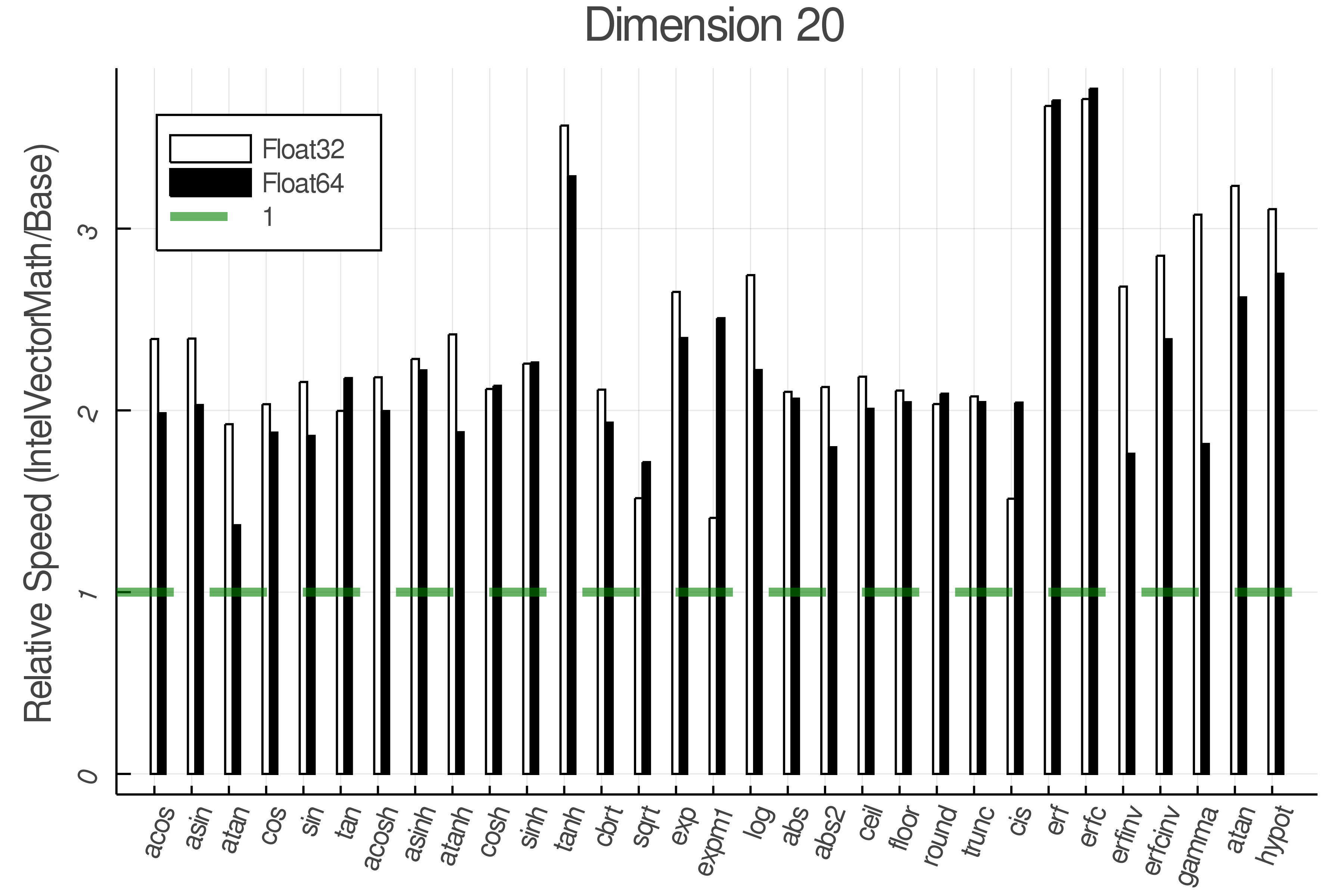
+ Real Functions - Full Benchmark Results
+
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+
+
+
+
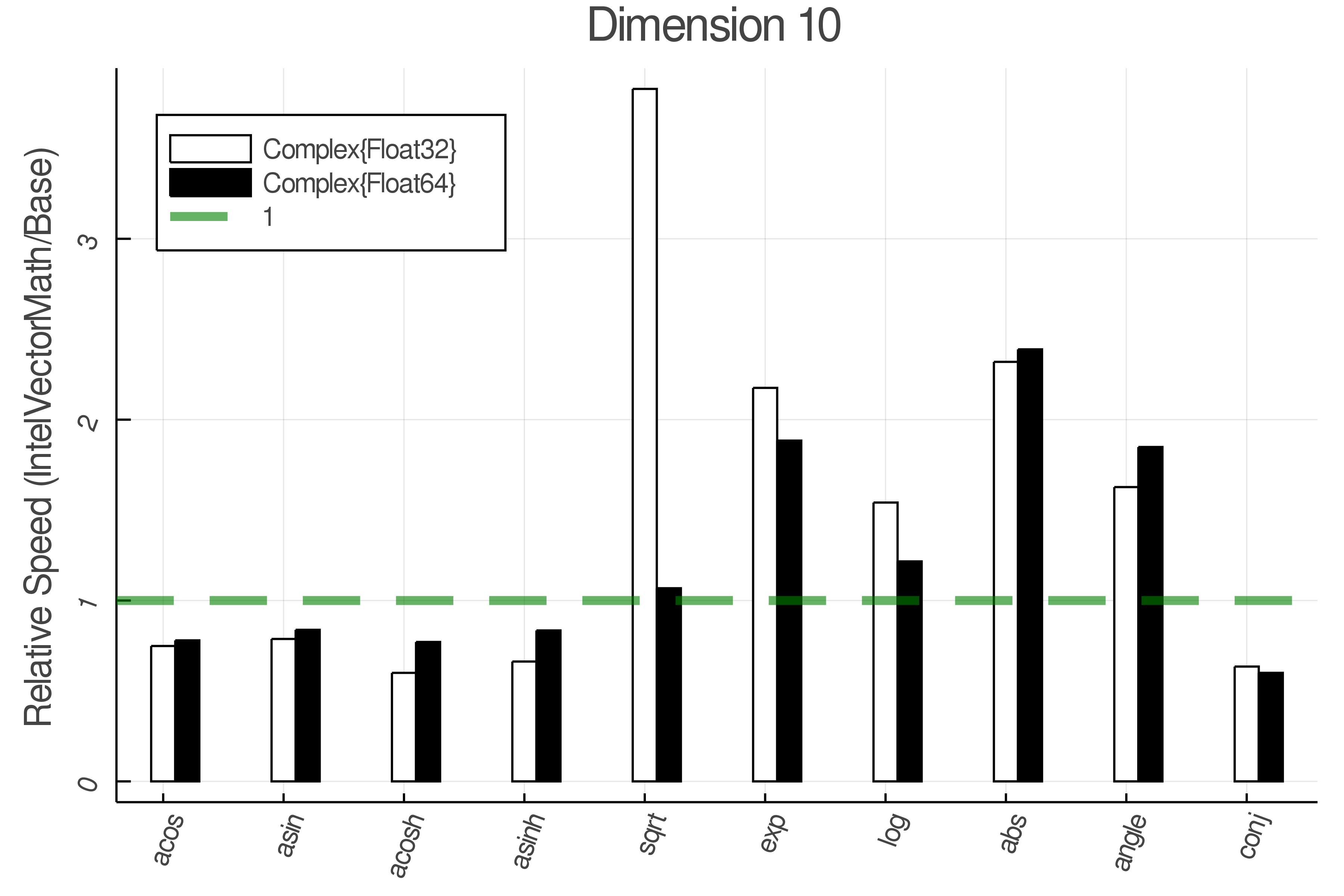
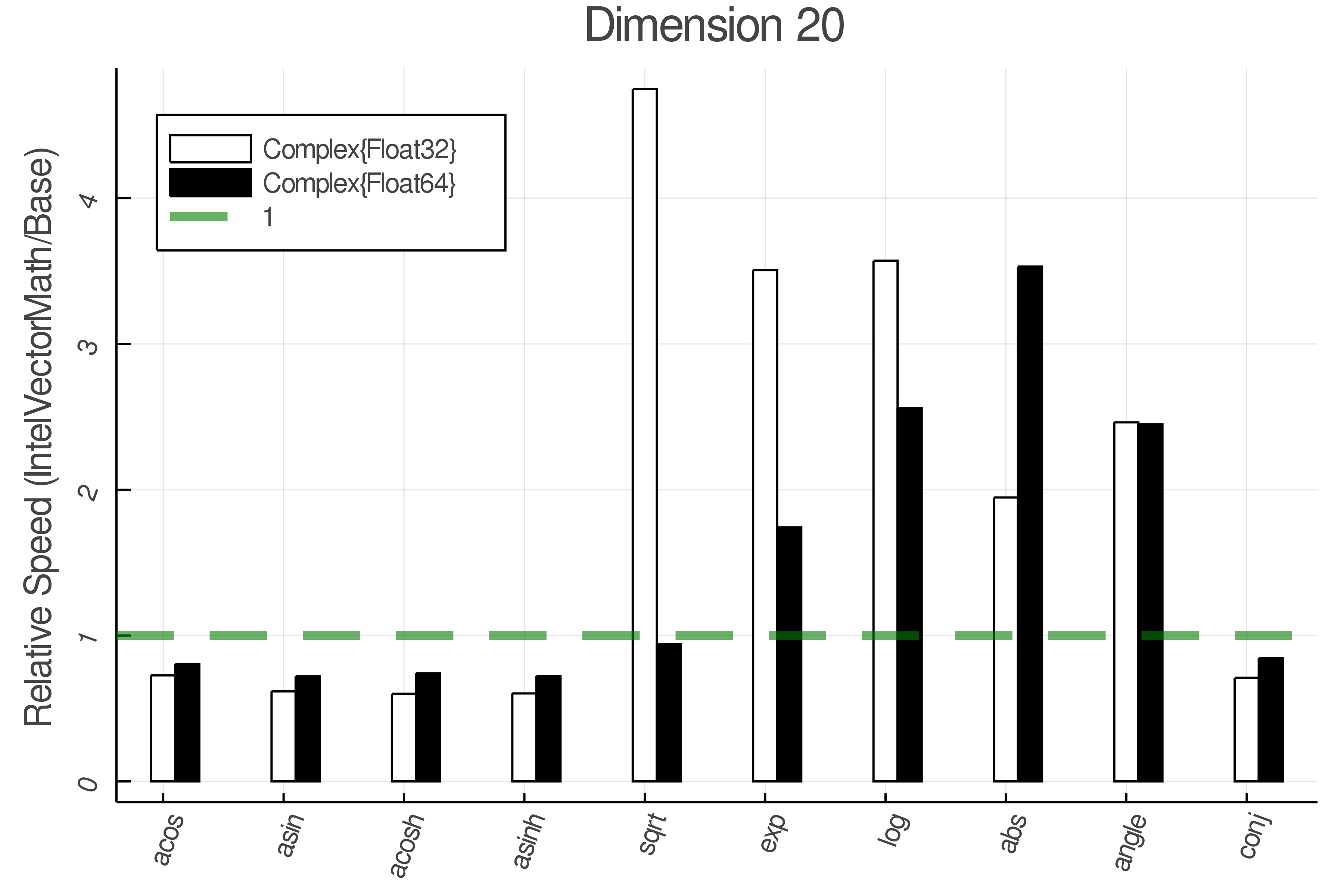
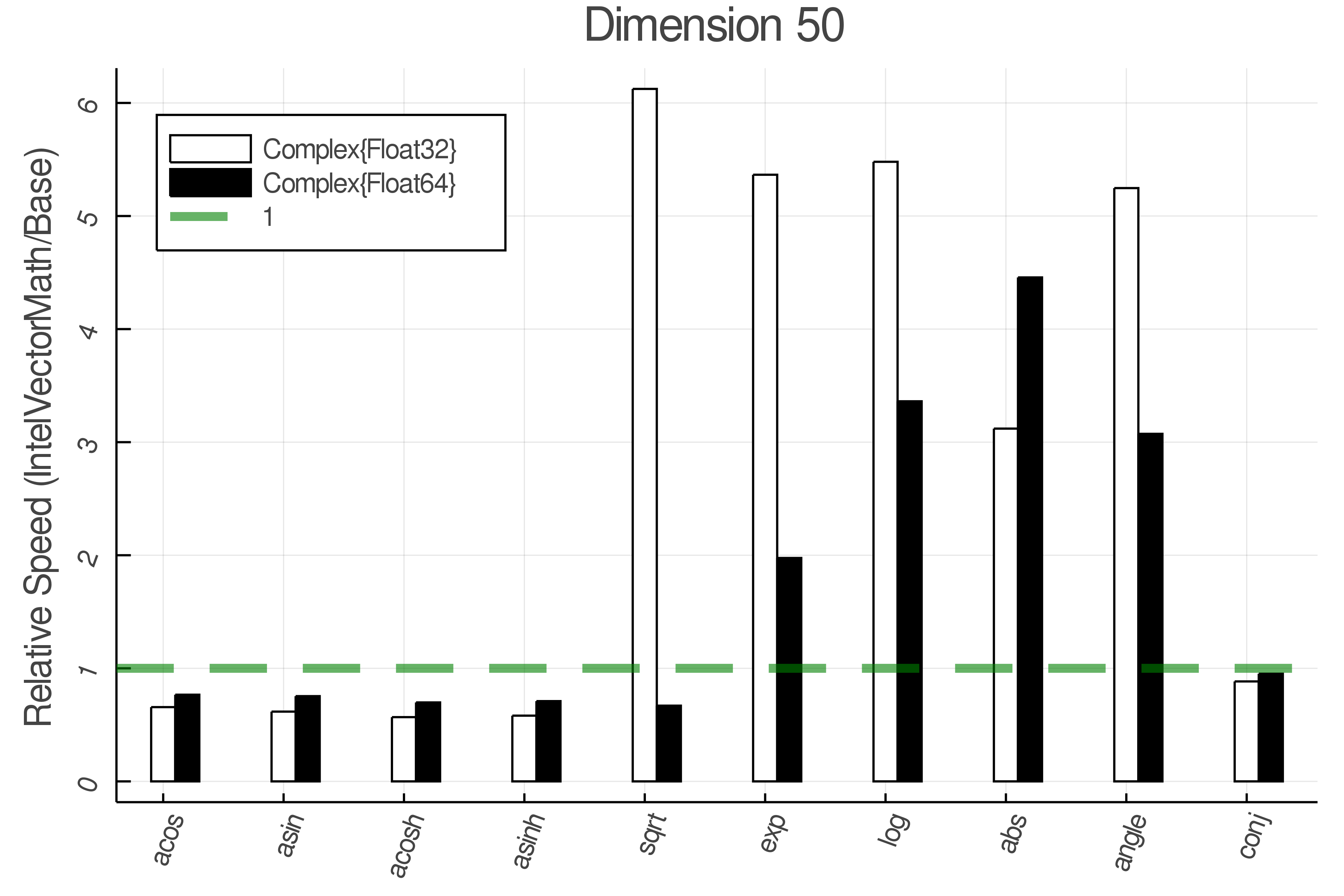
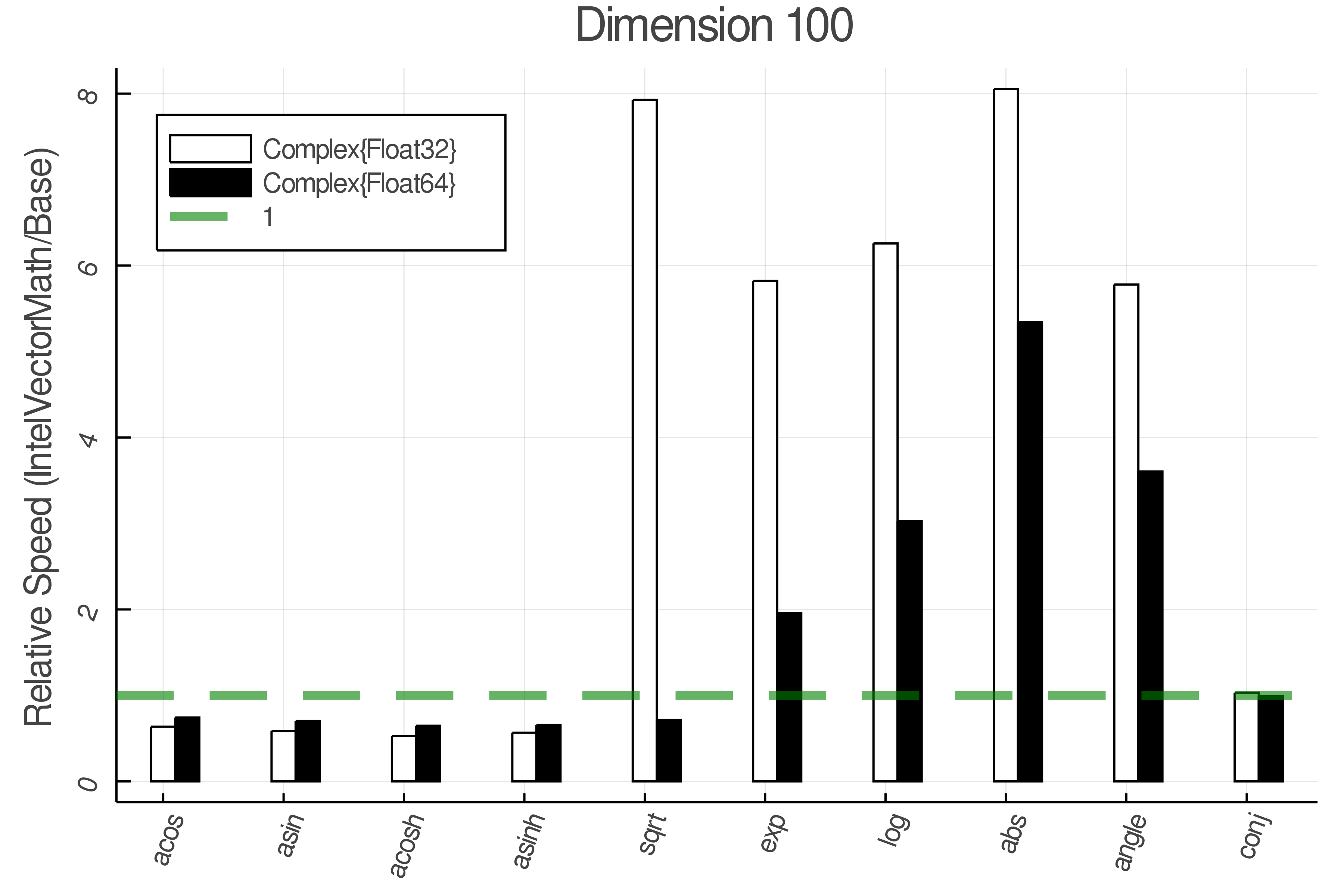
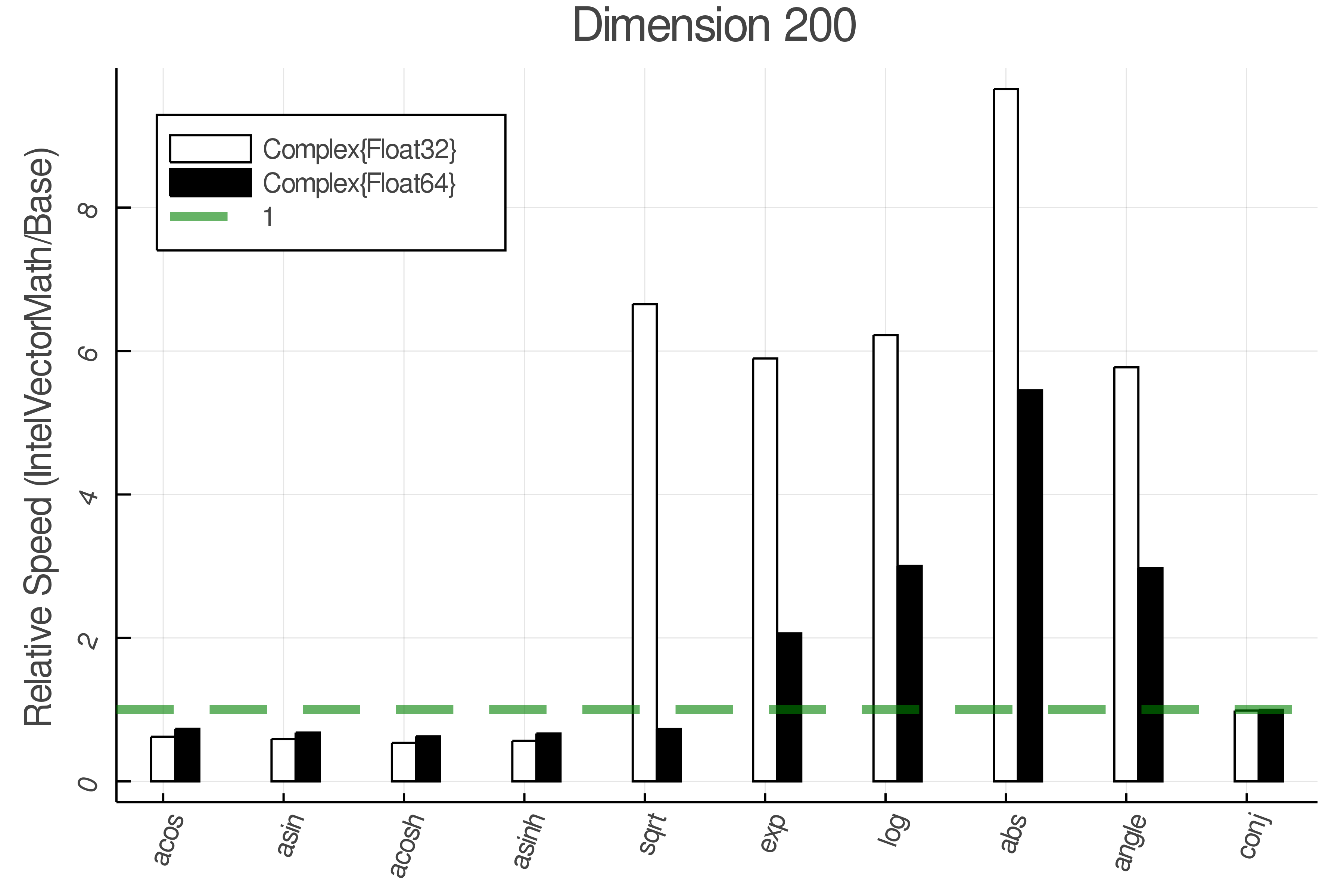
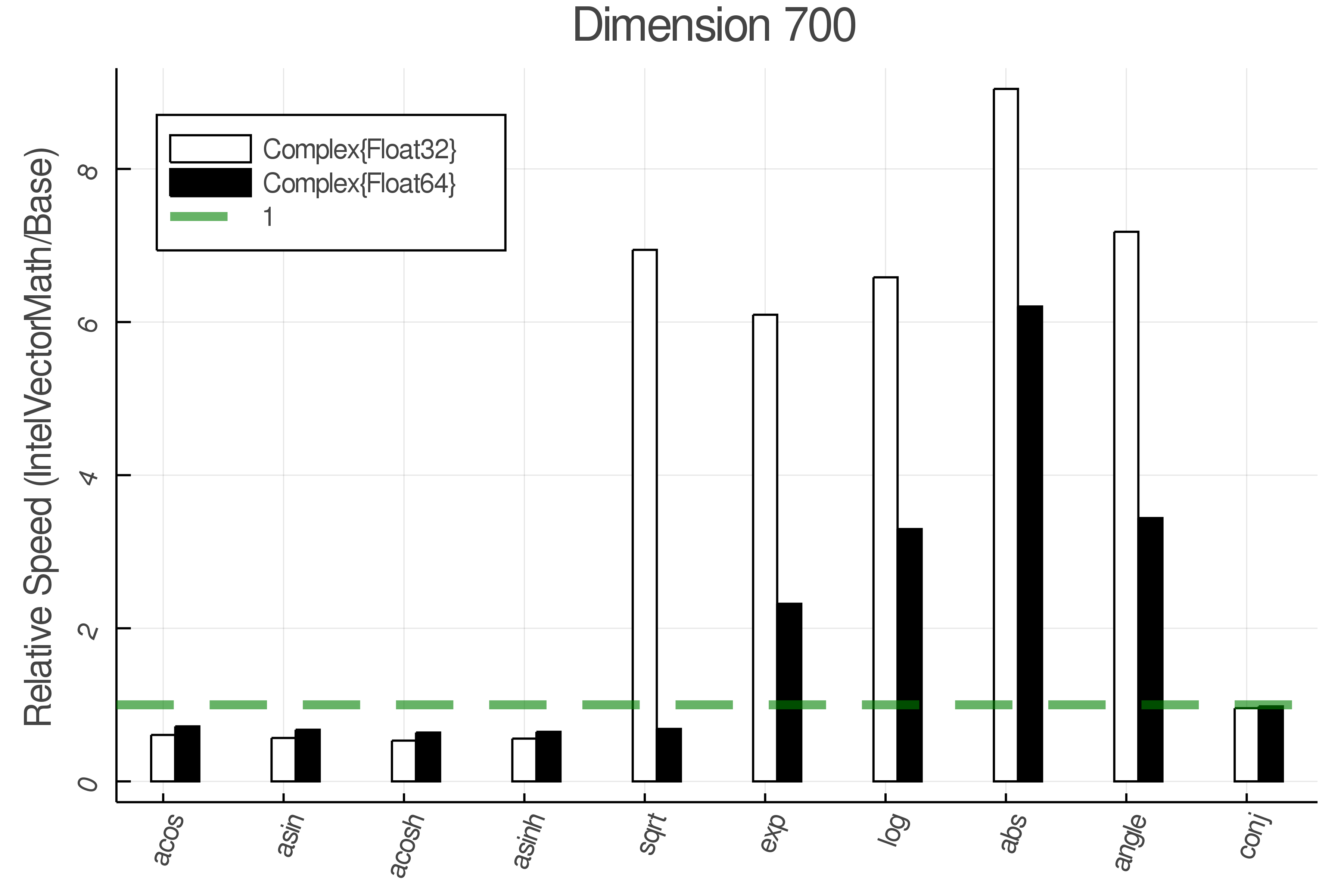
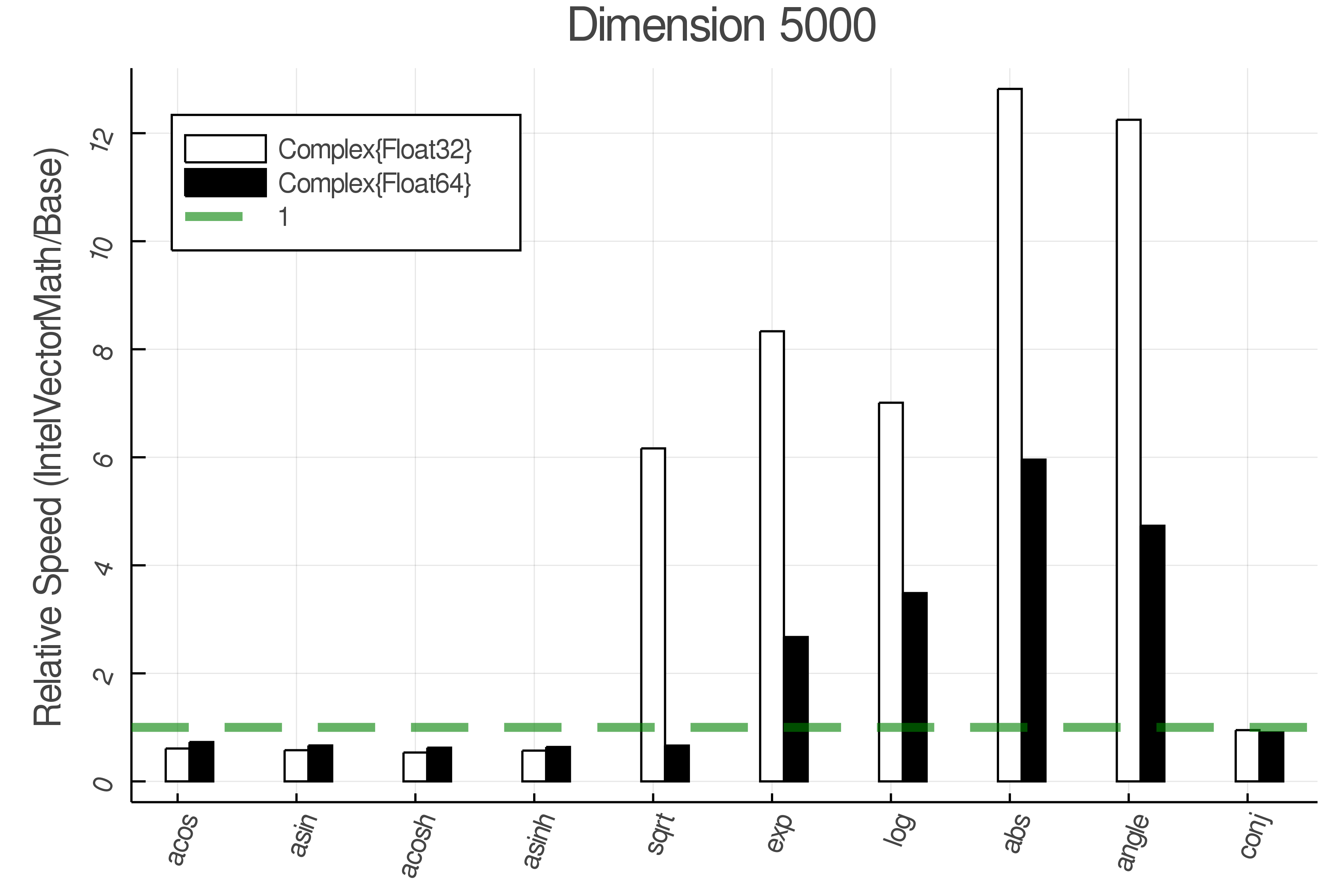
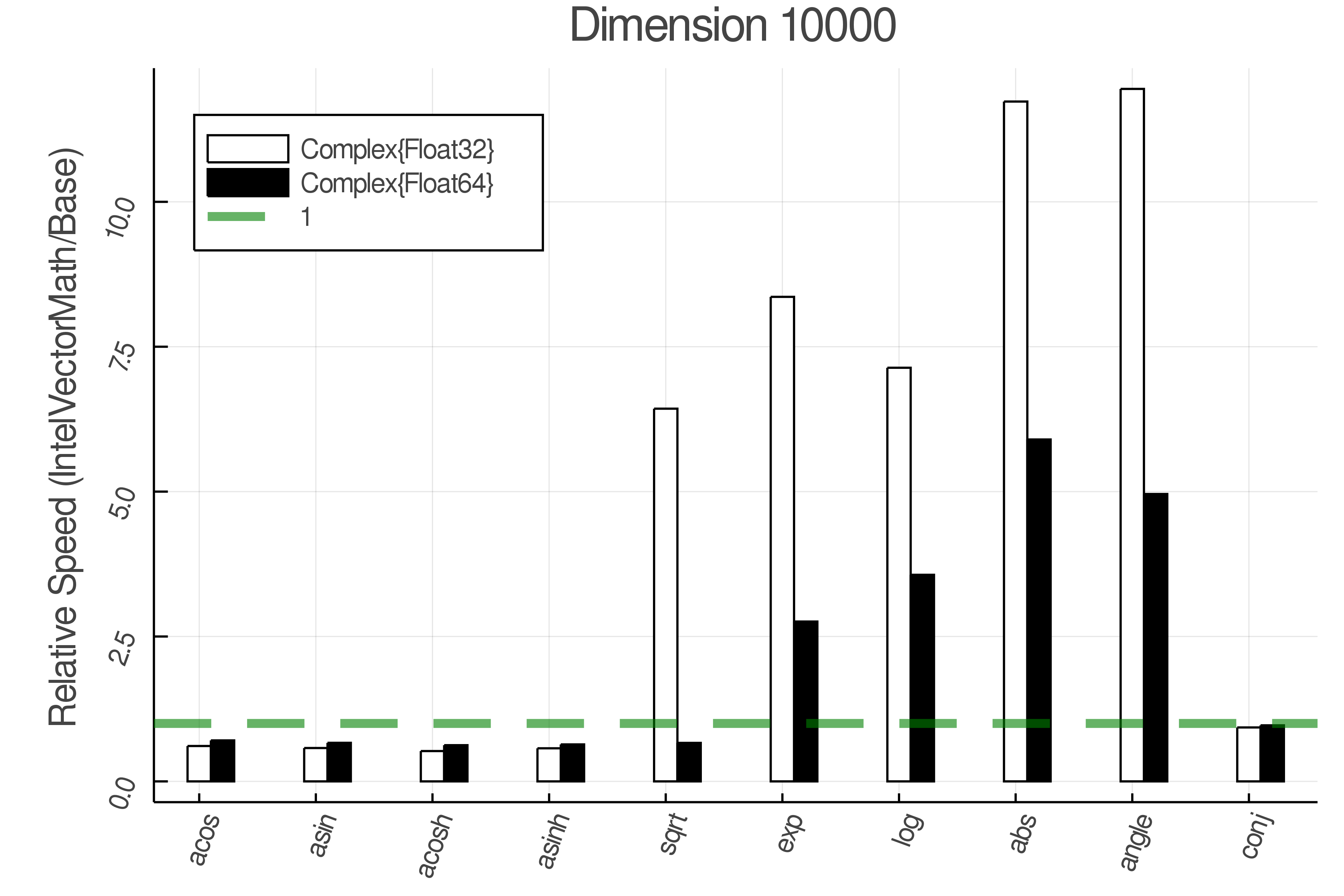
+ Complex Functions - Full Benchmark Results
+
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+
+
+
+
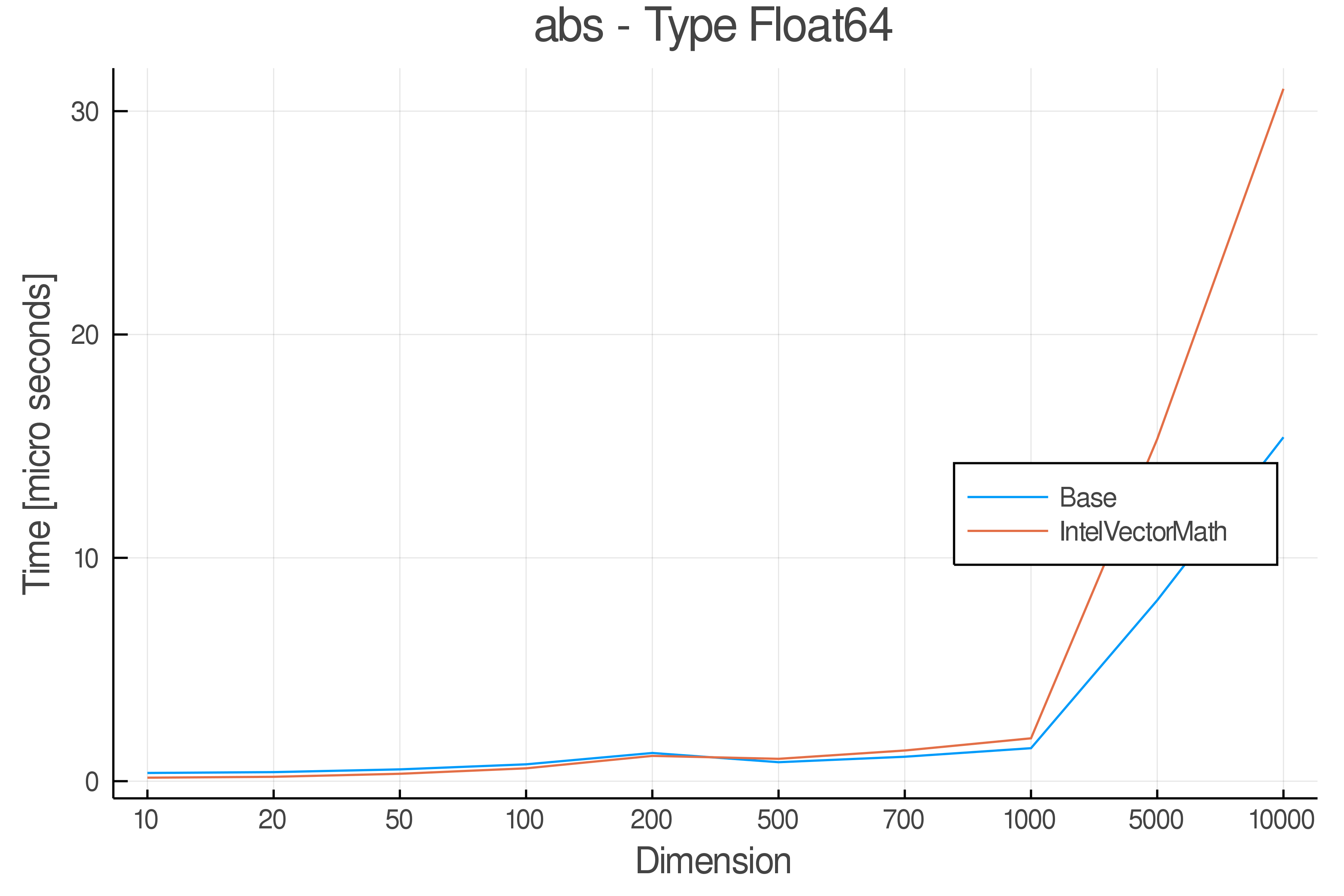
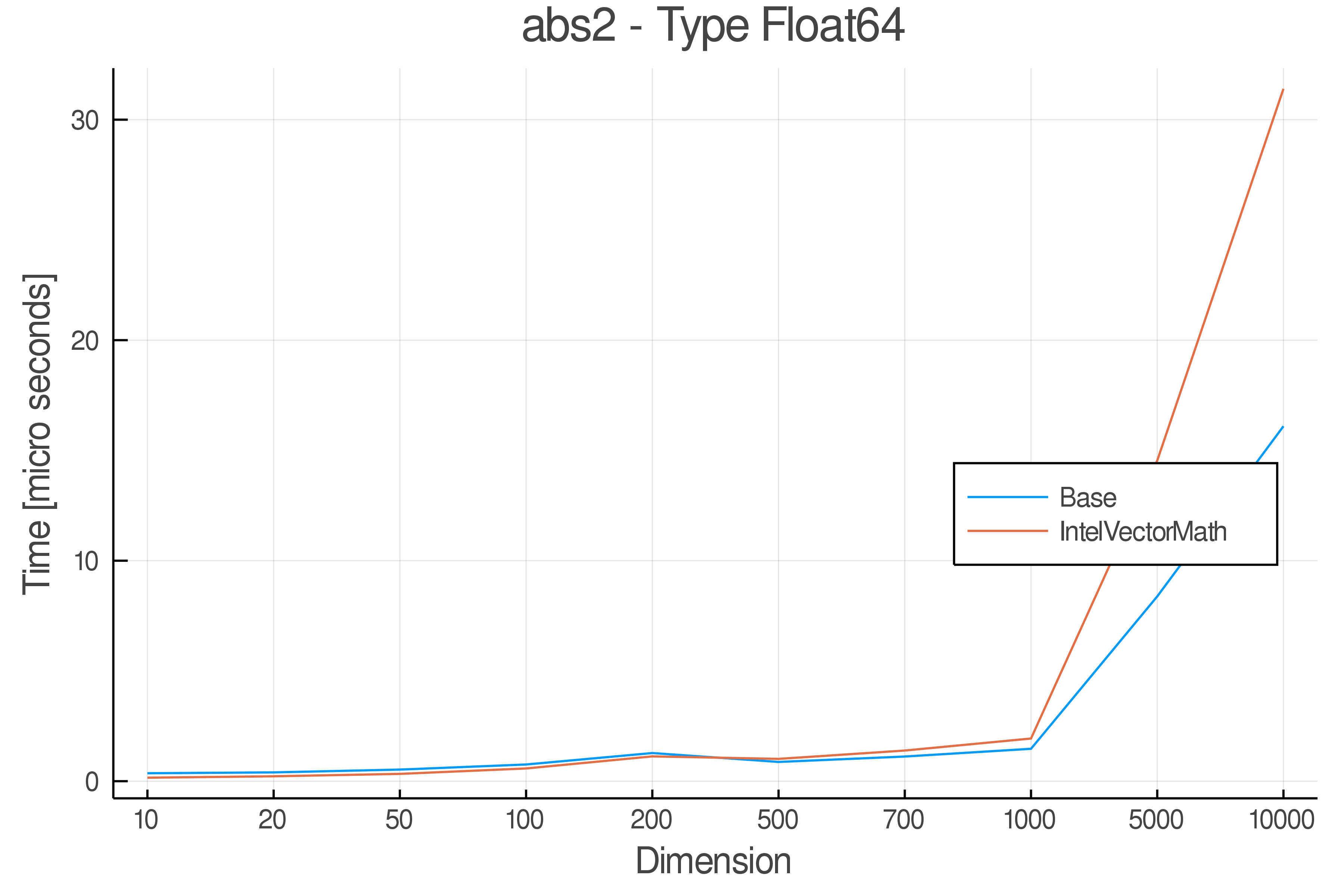
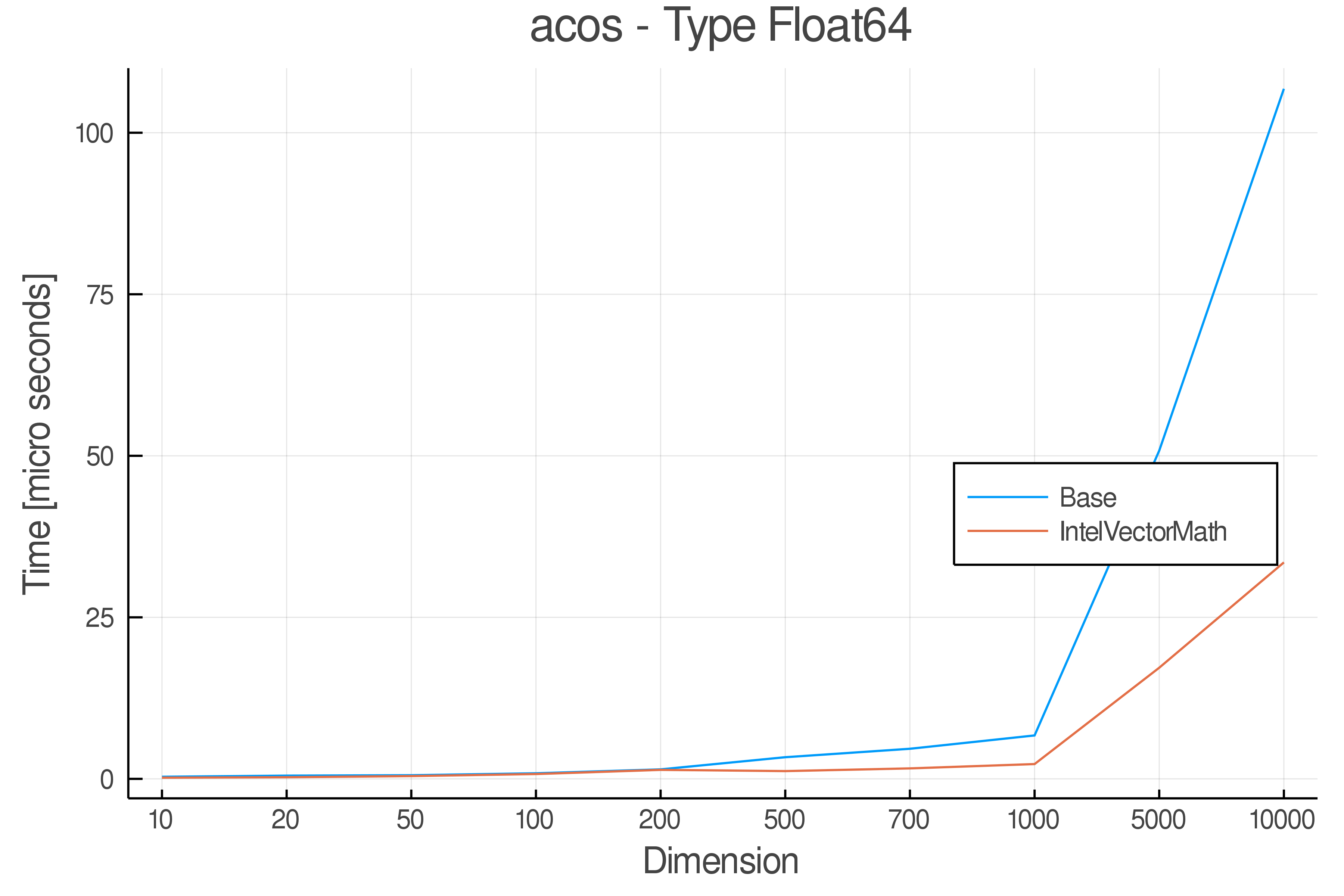
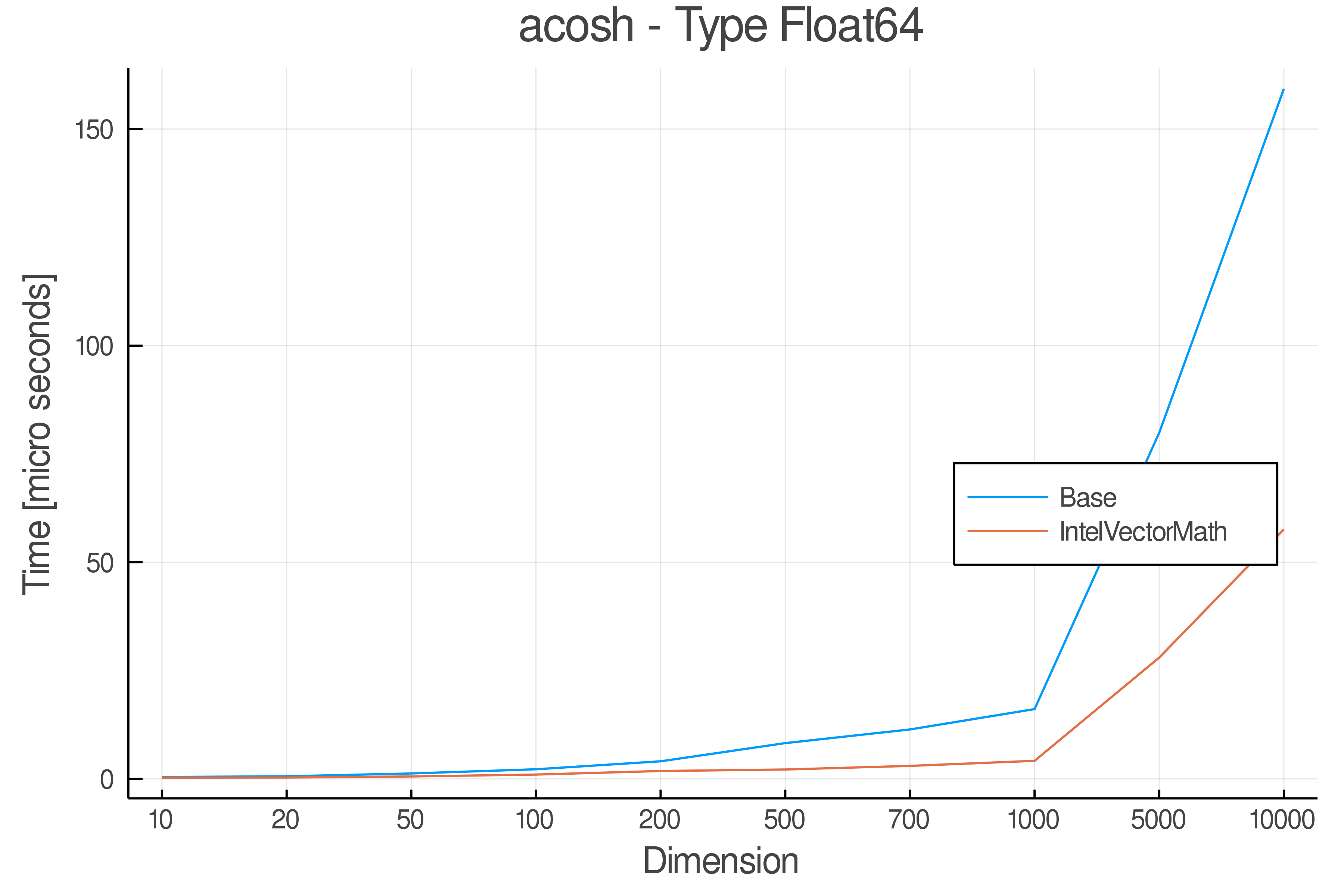
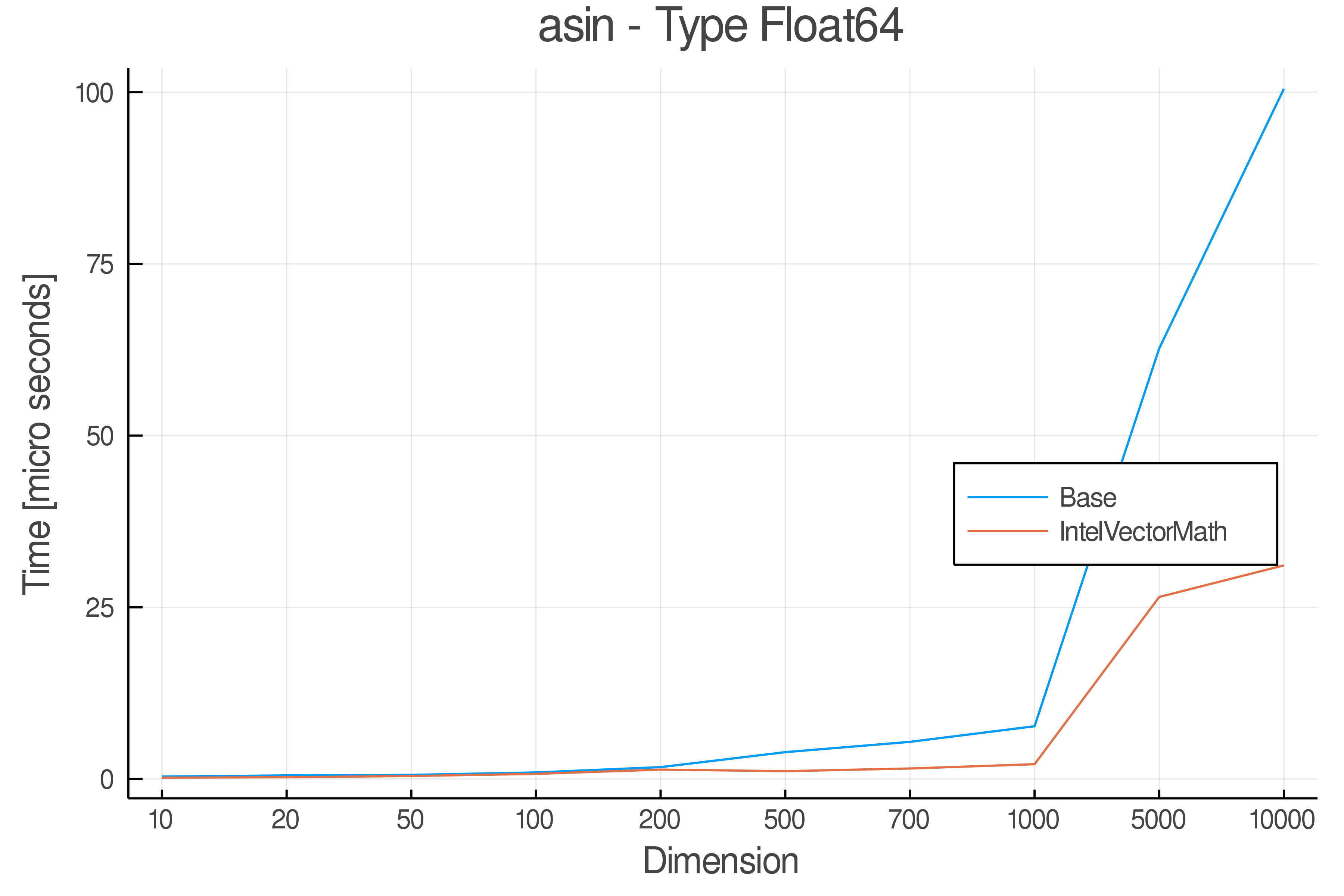
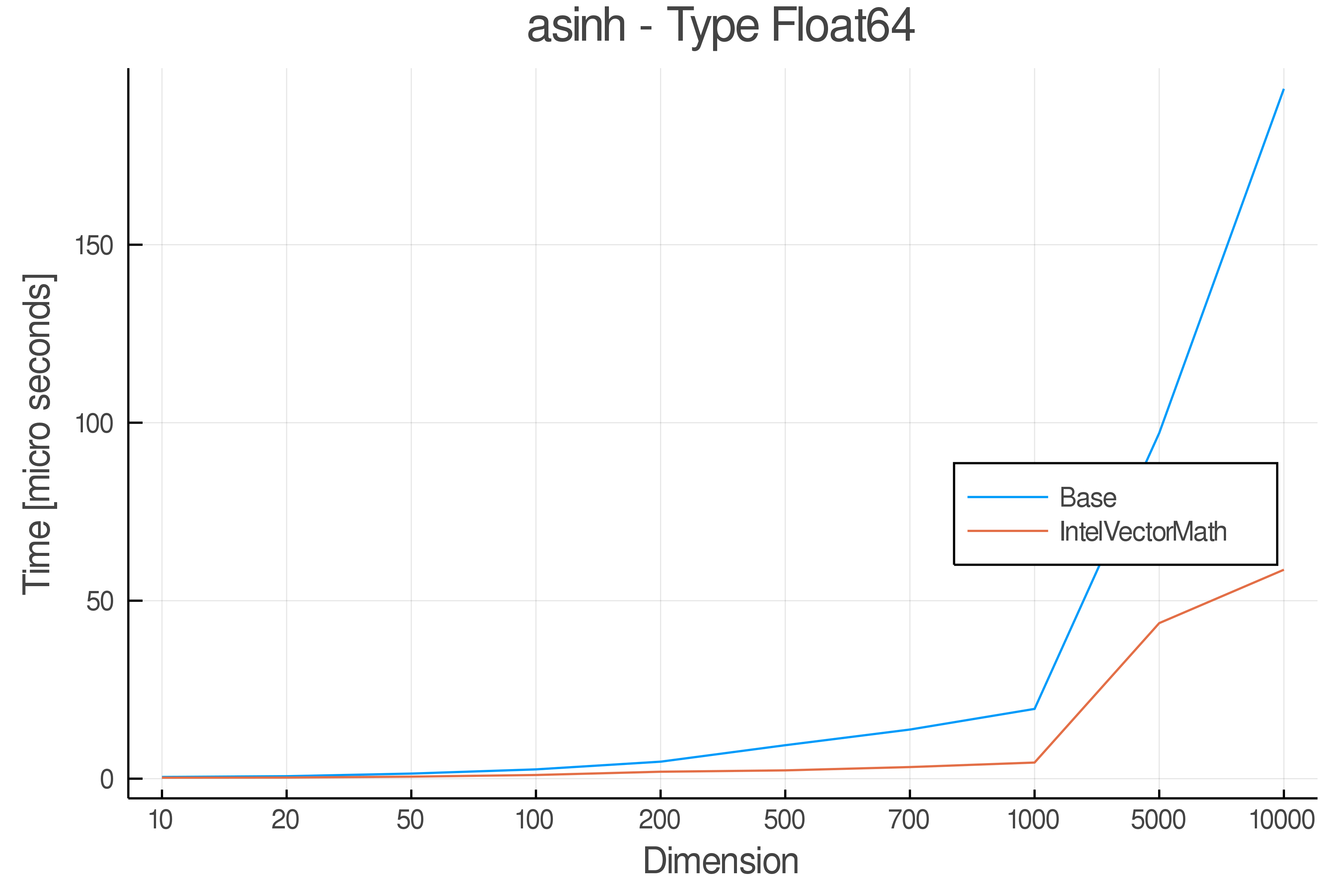
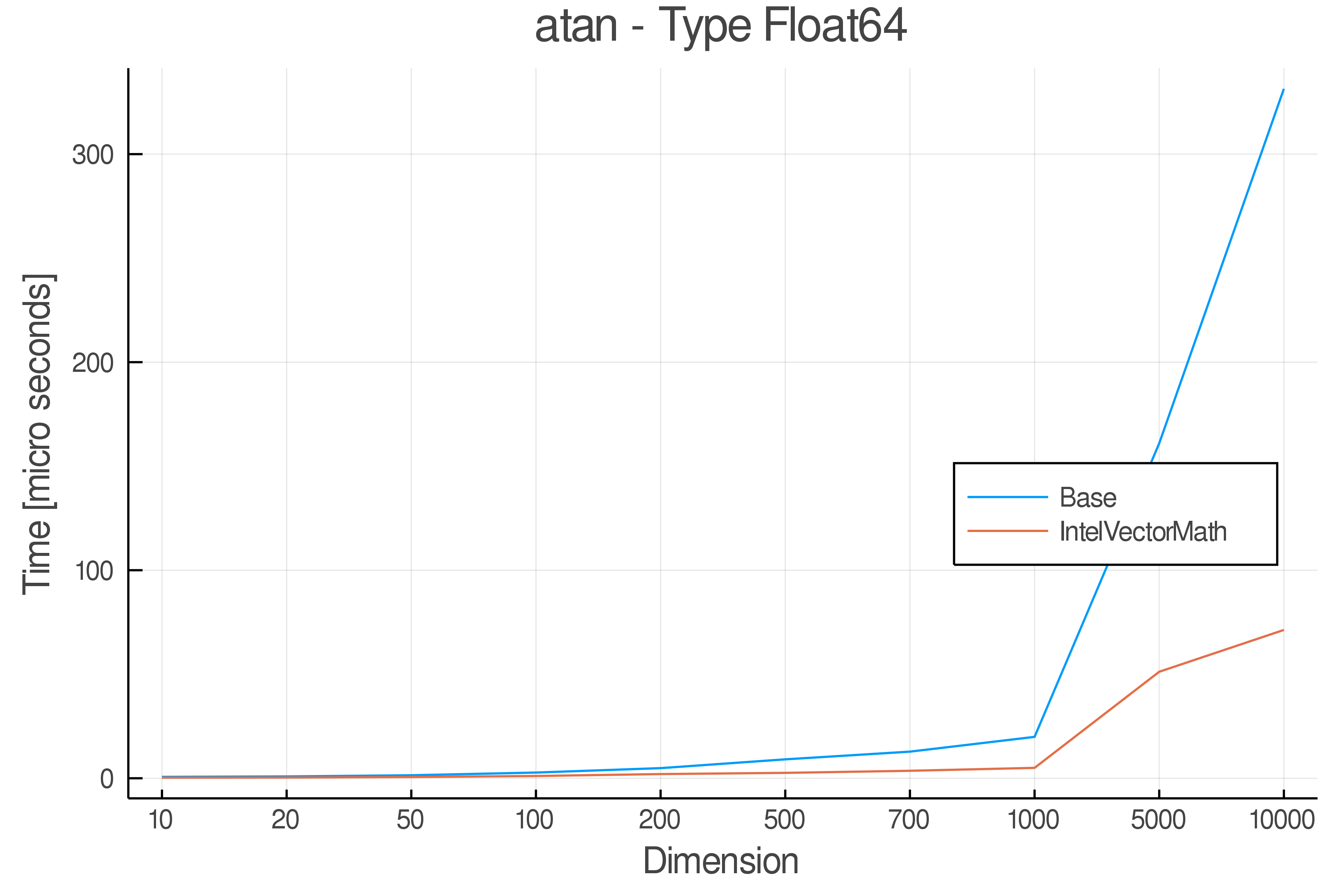
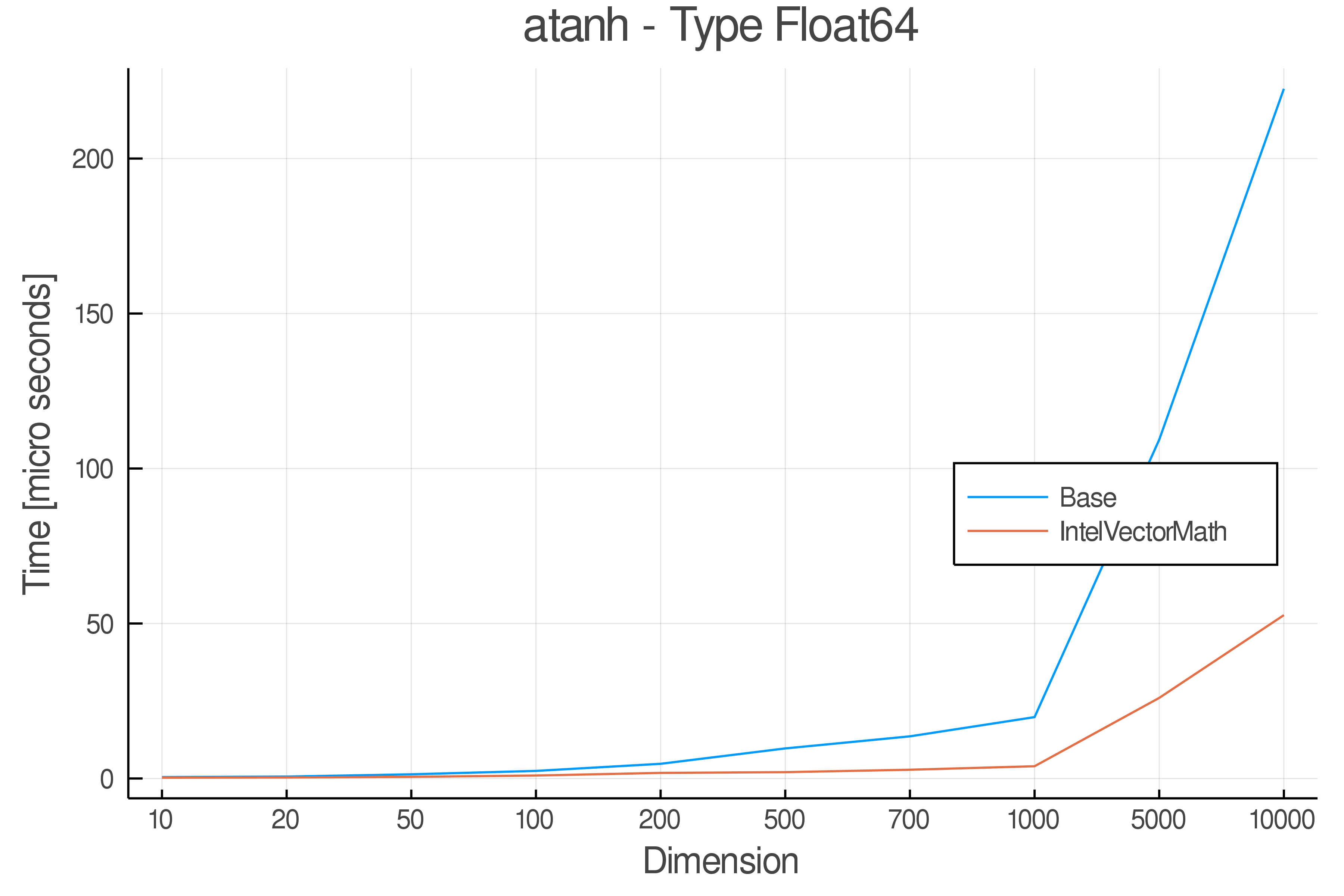
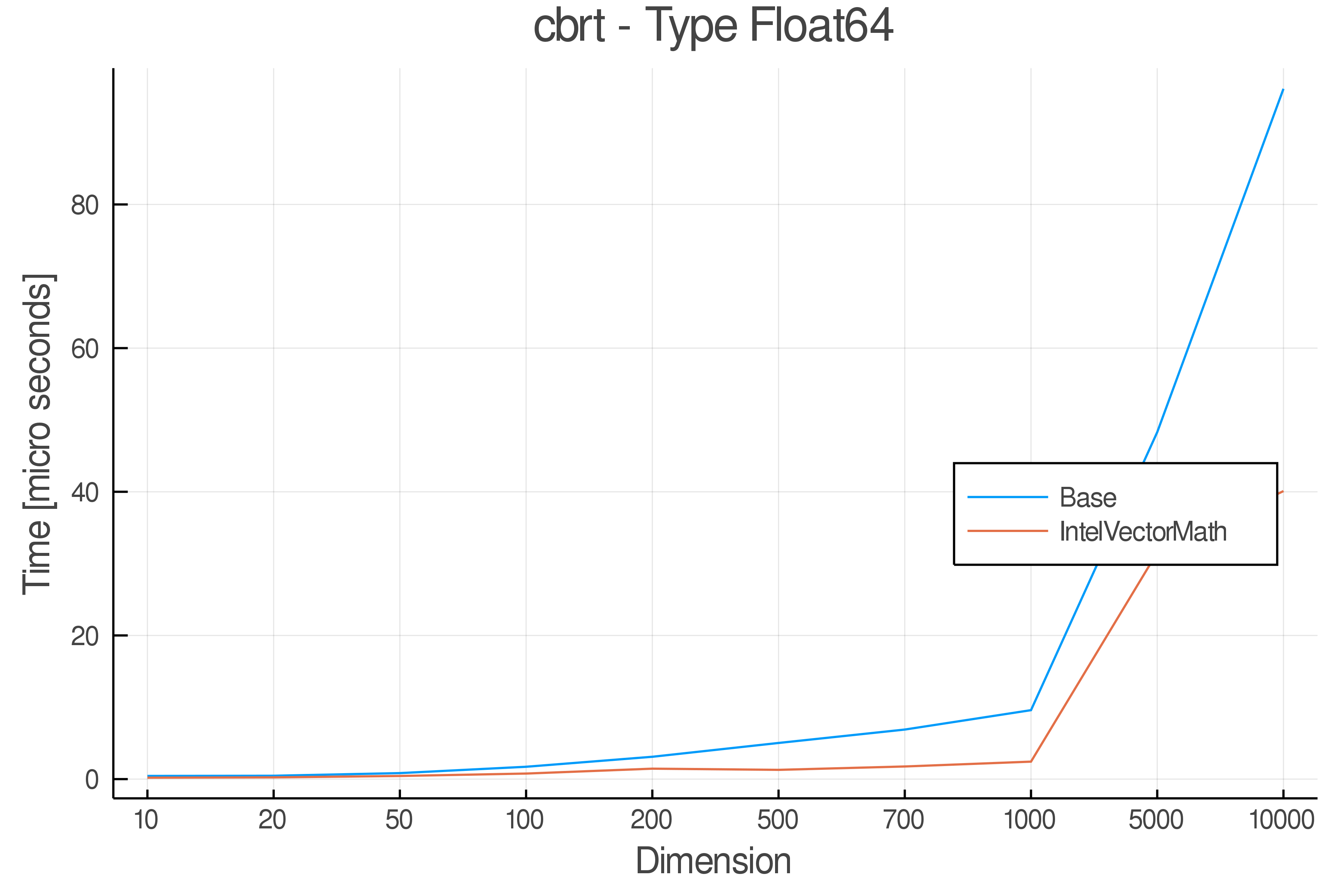
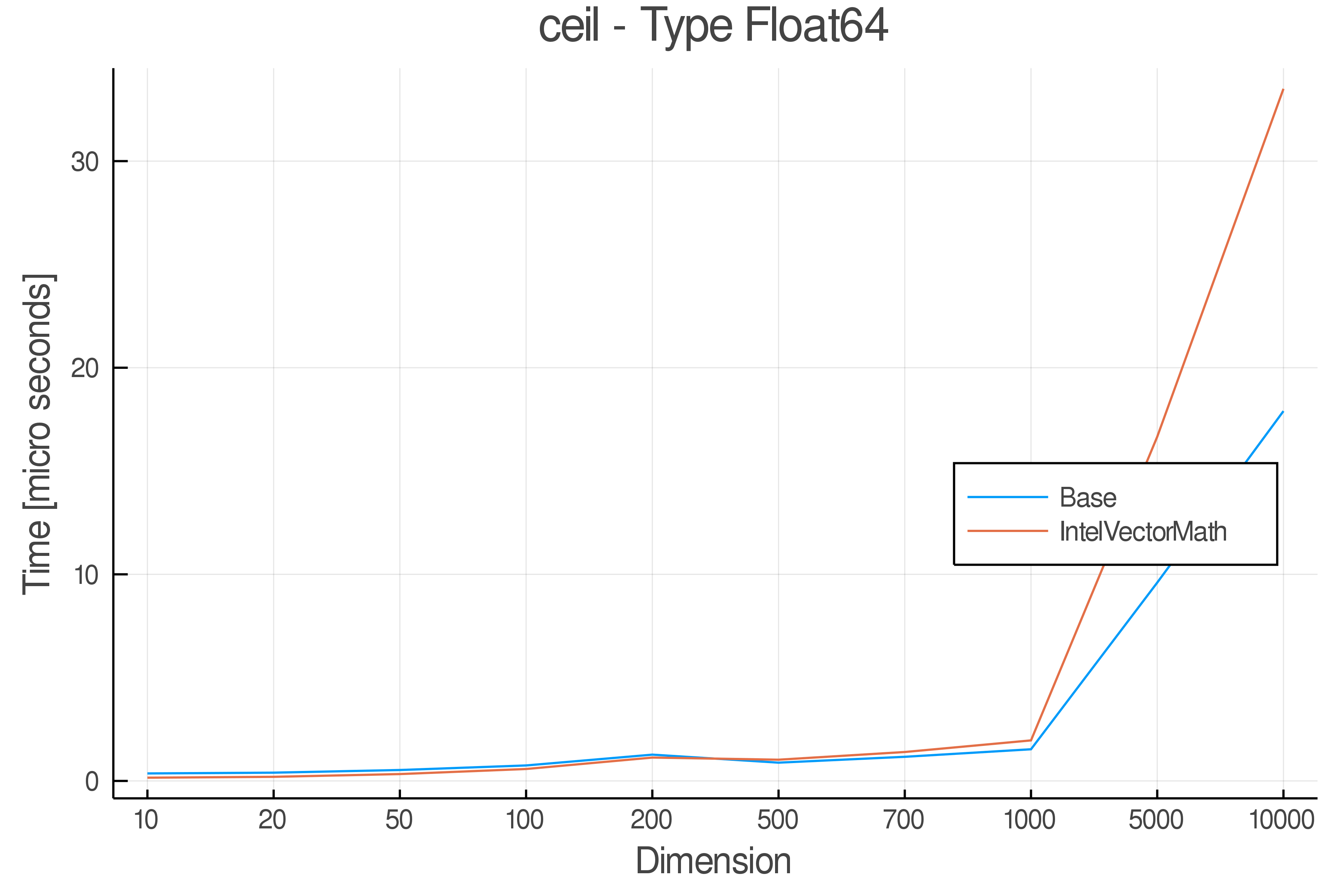
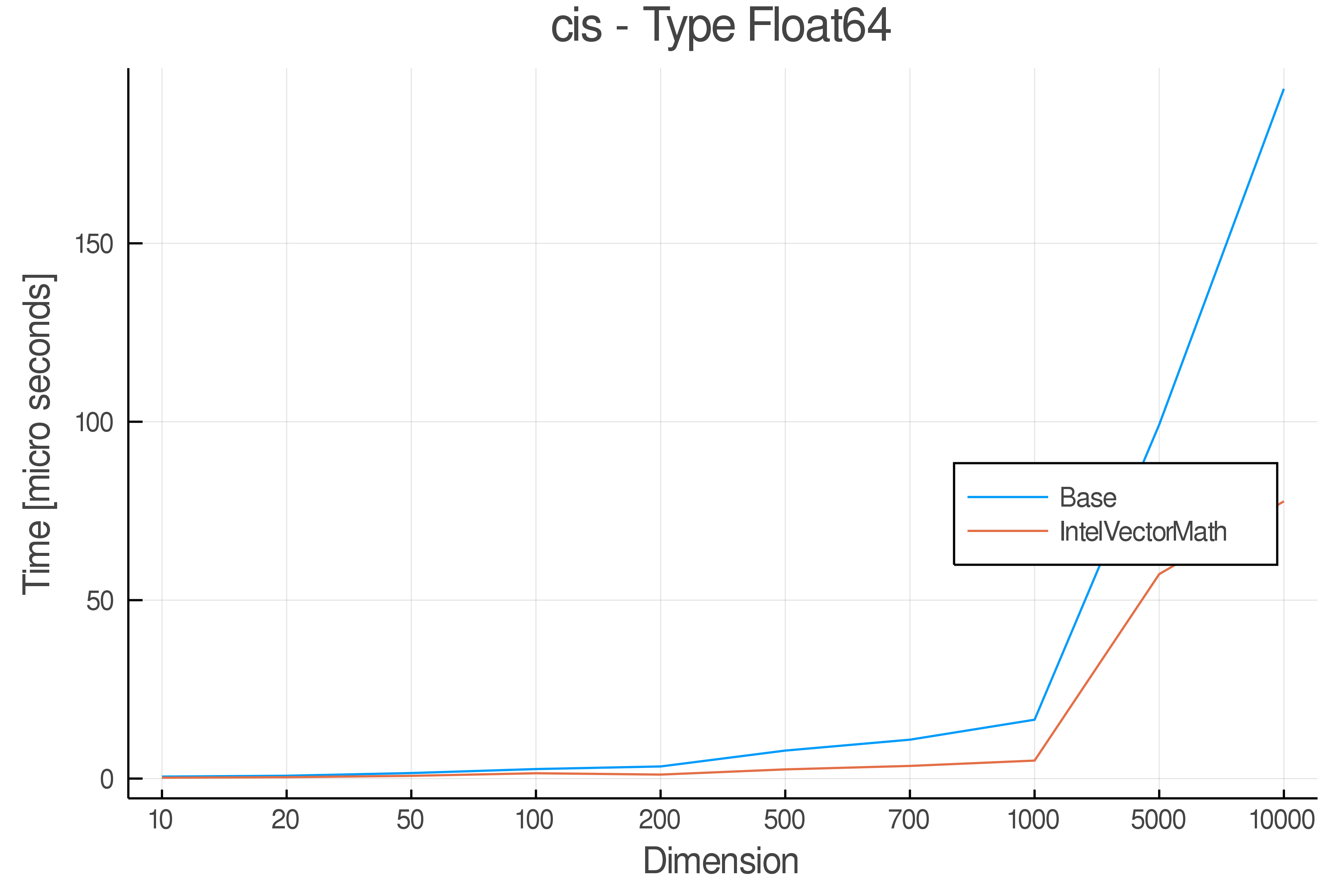
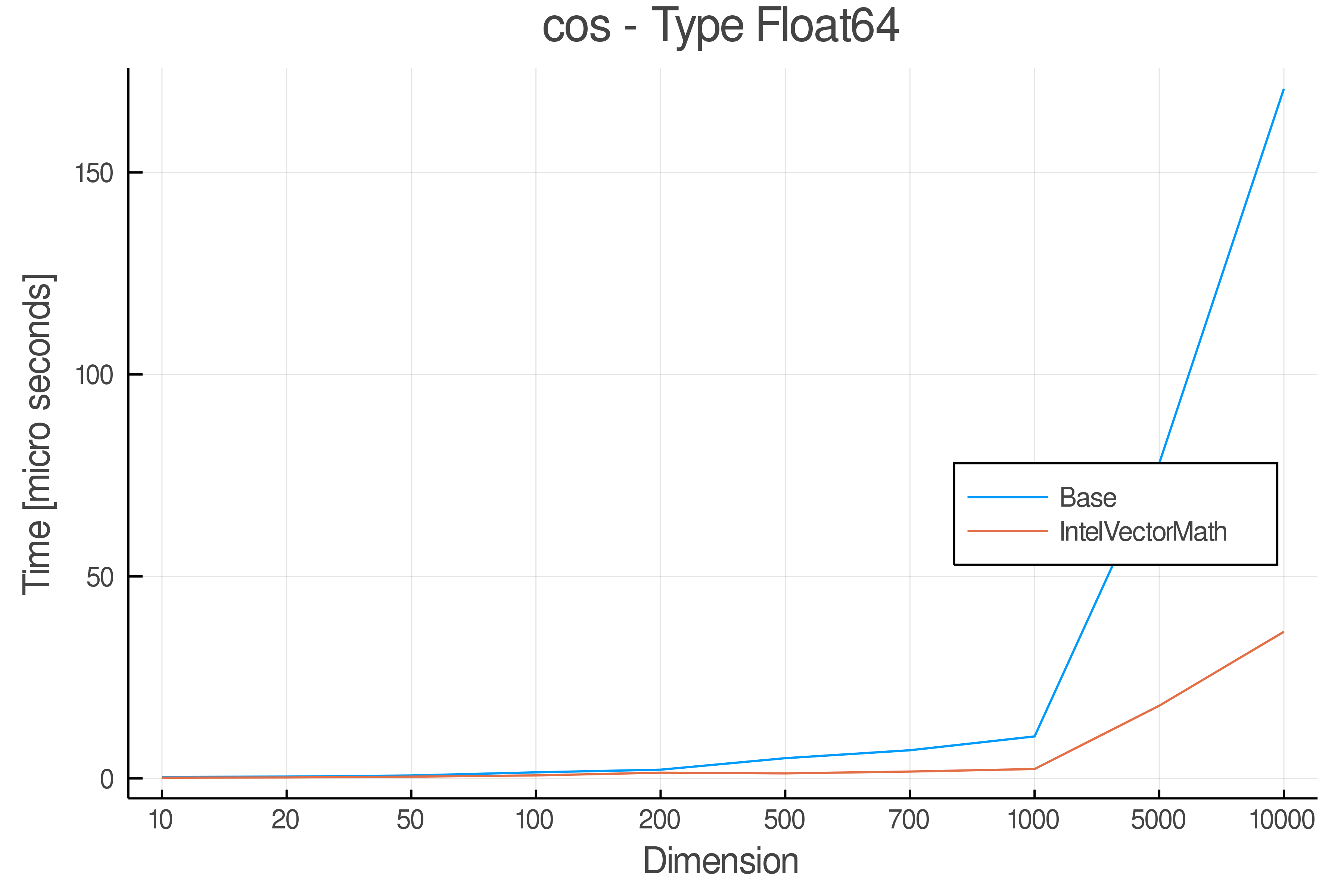
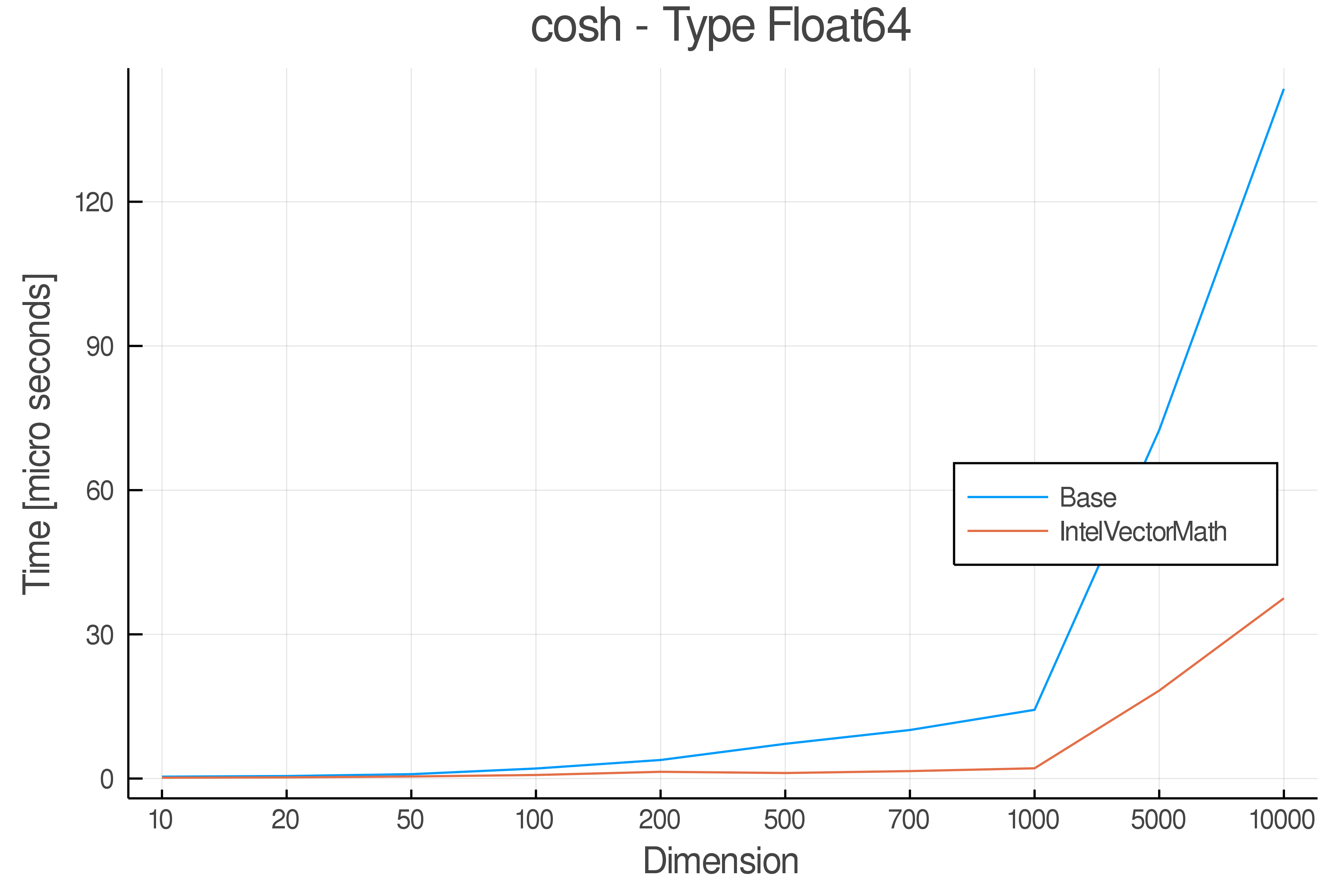
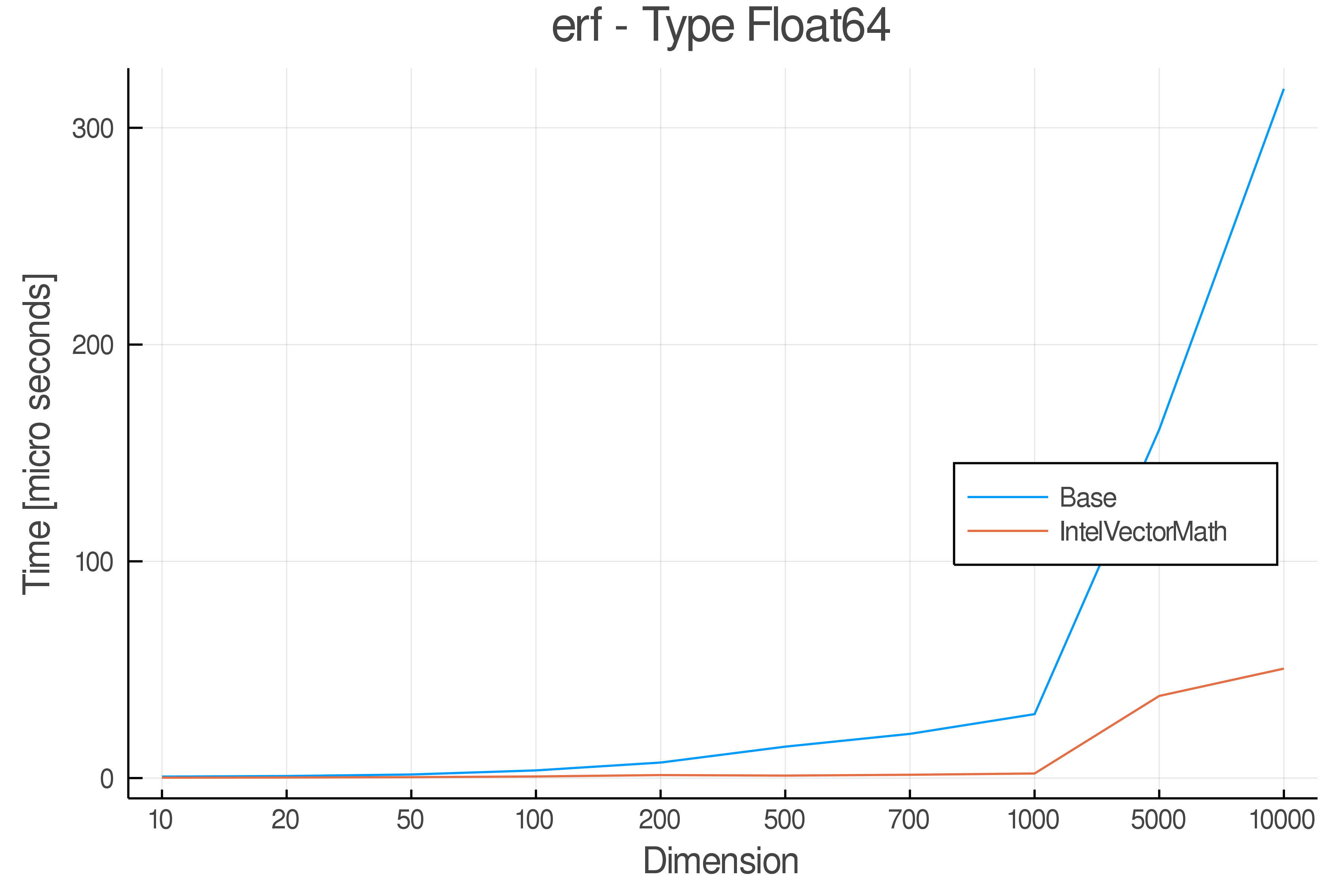
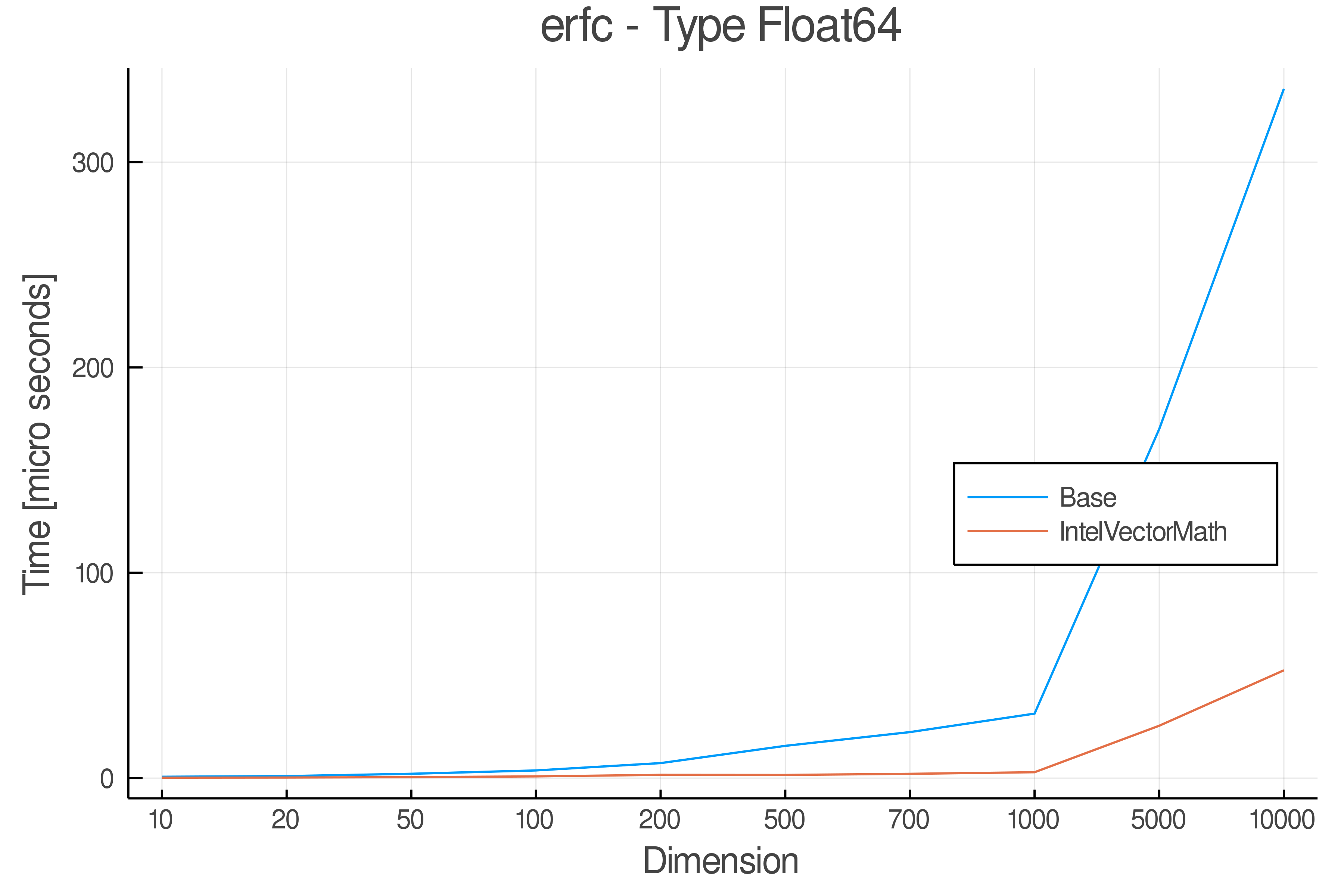
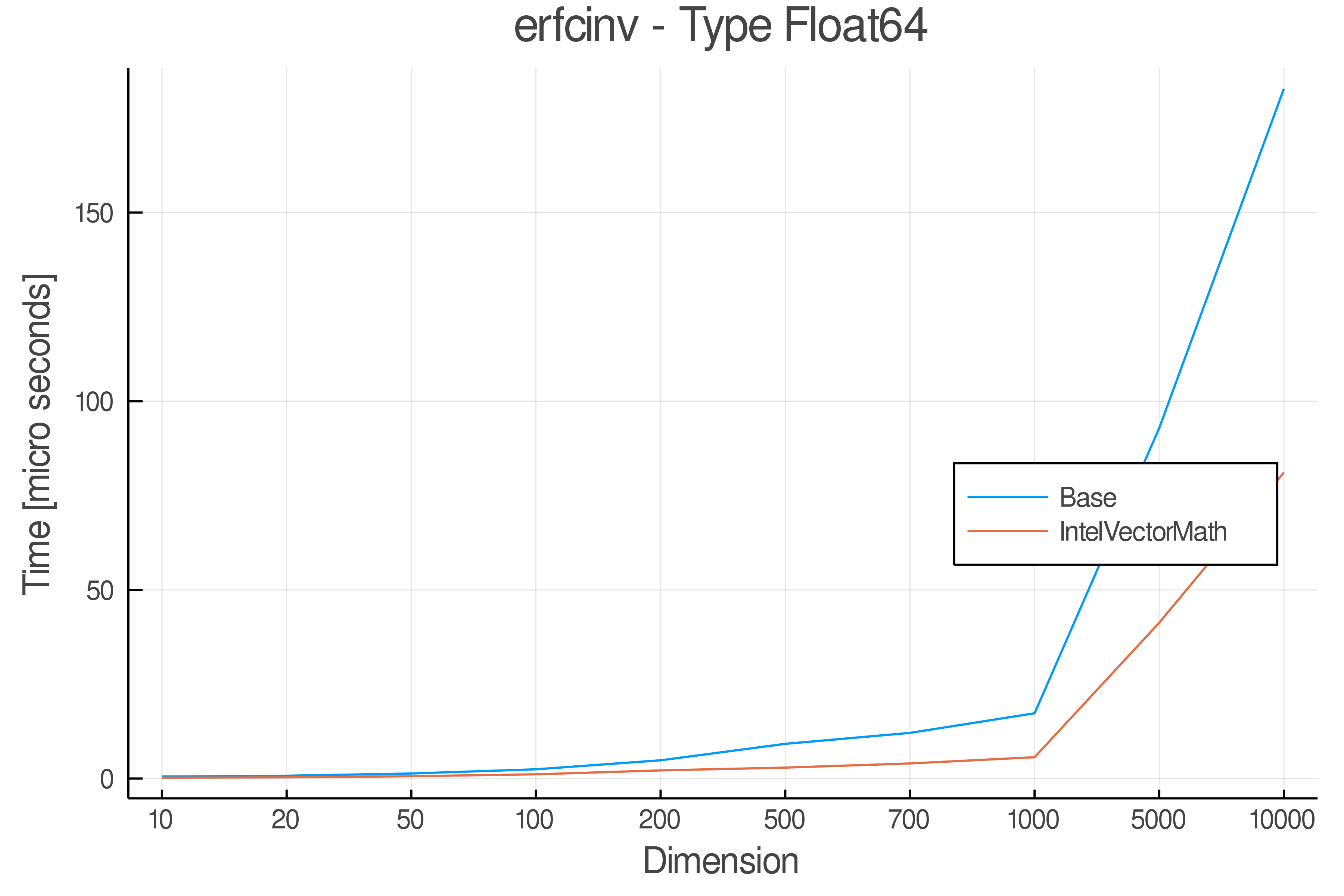
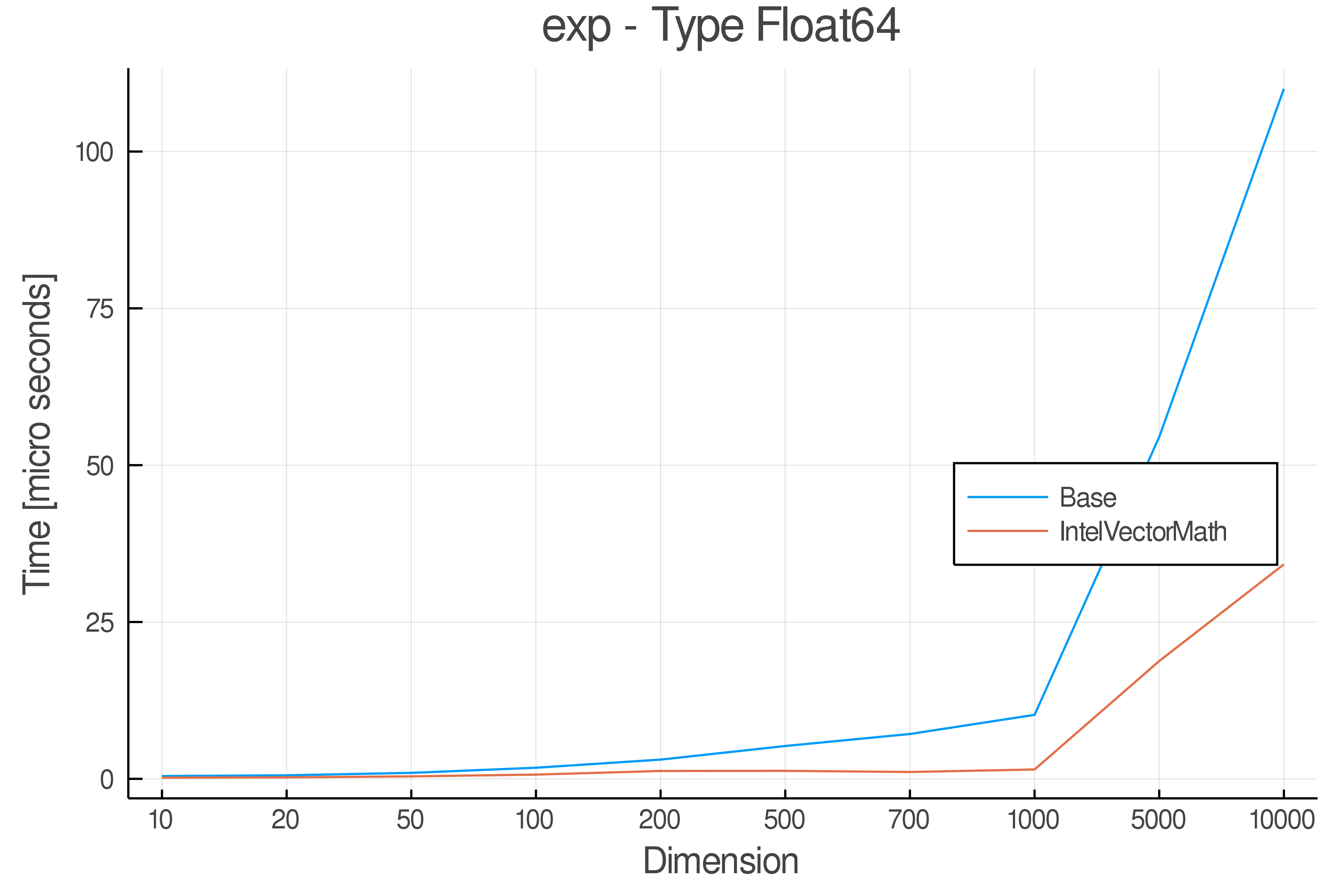
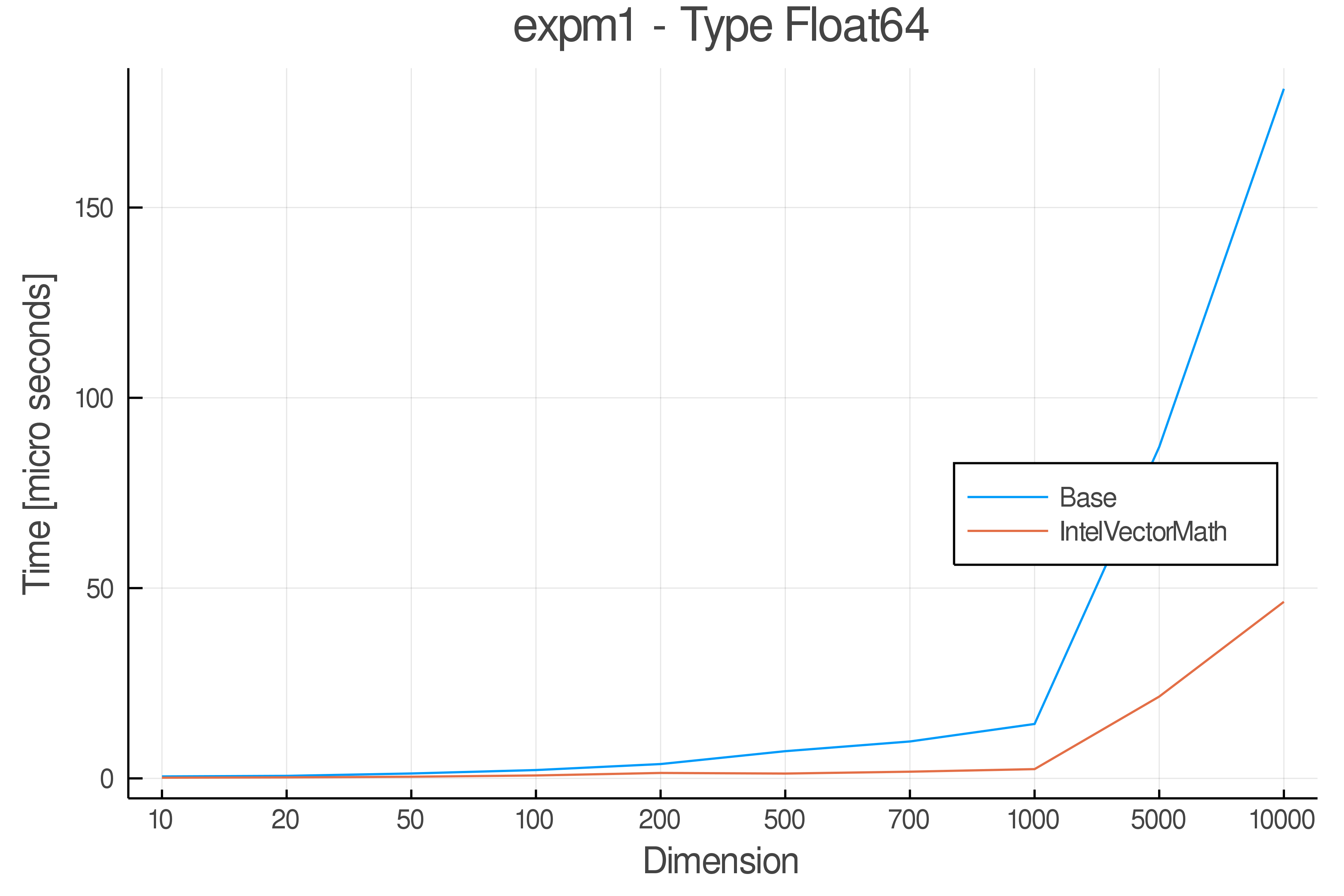
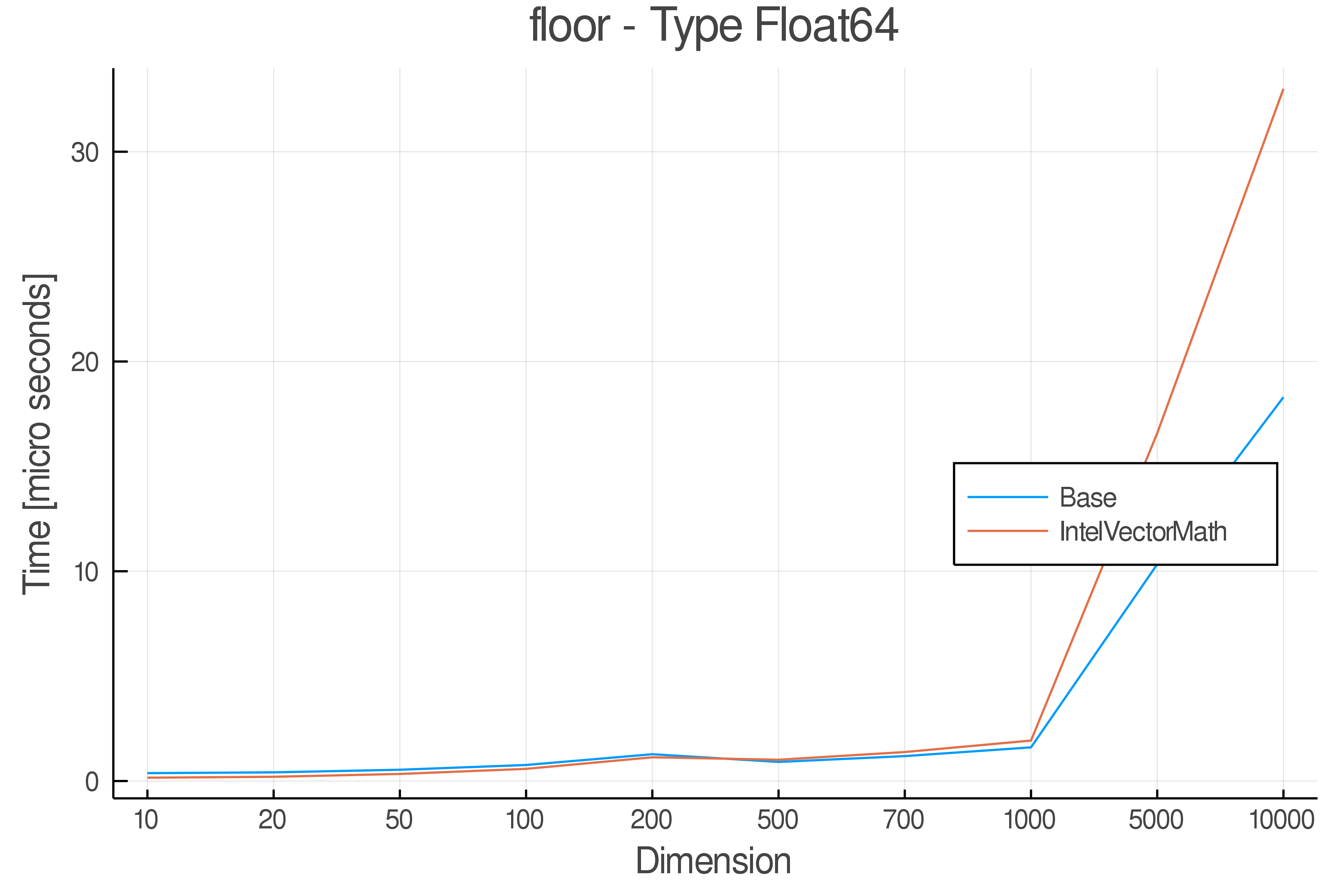
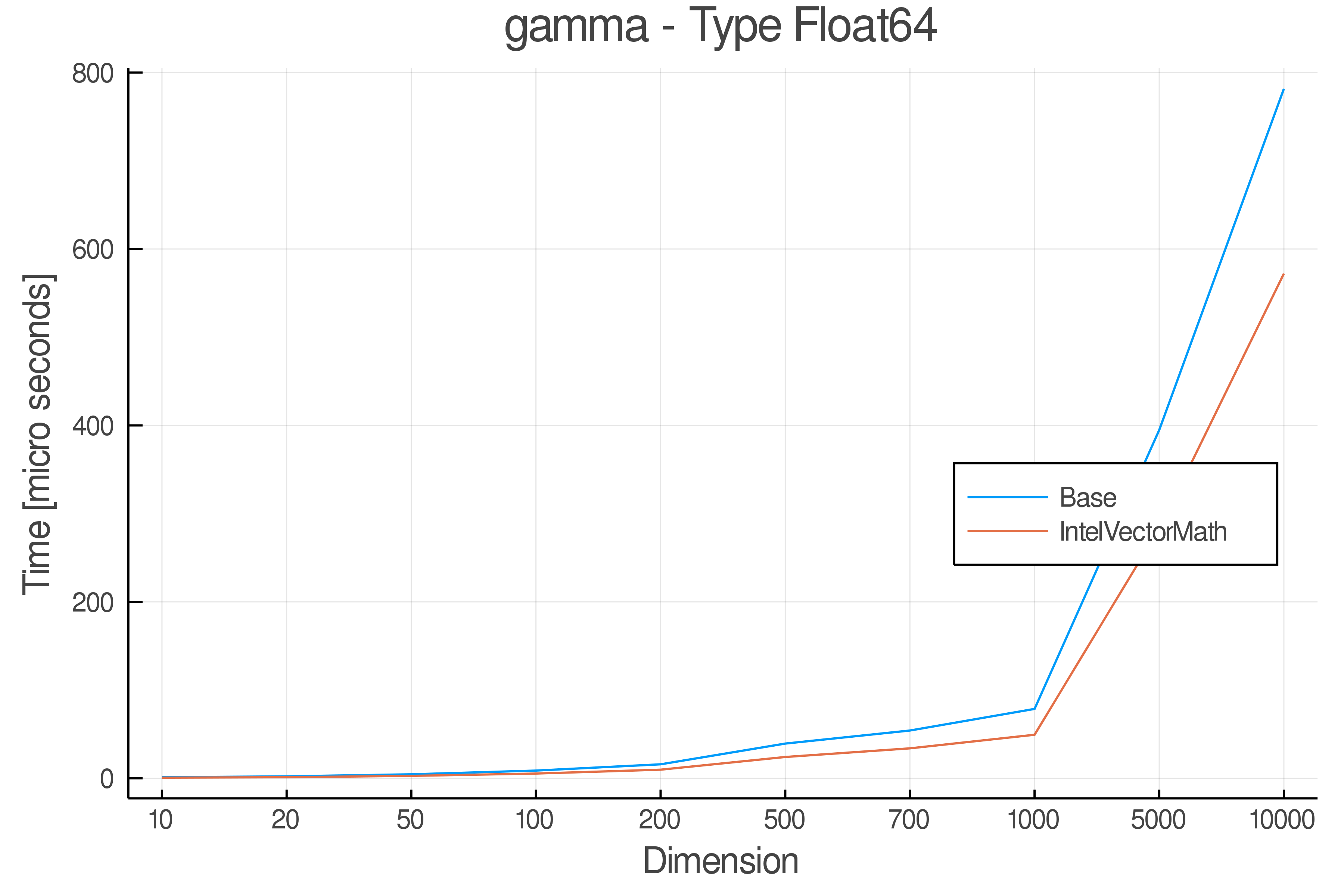
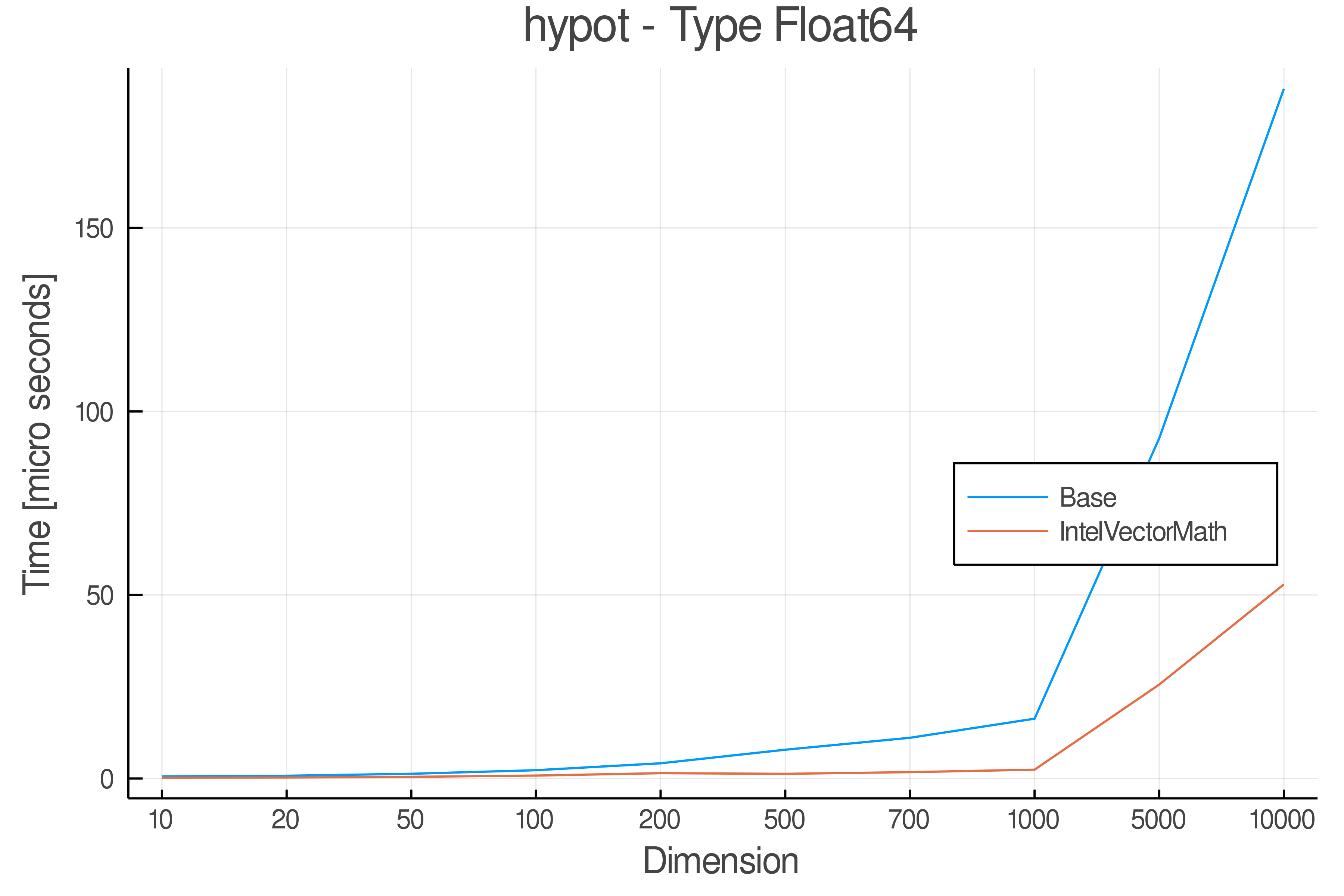
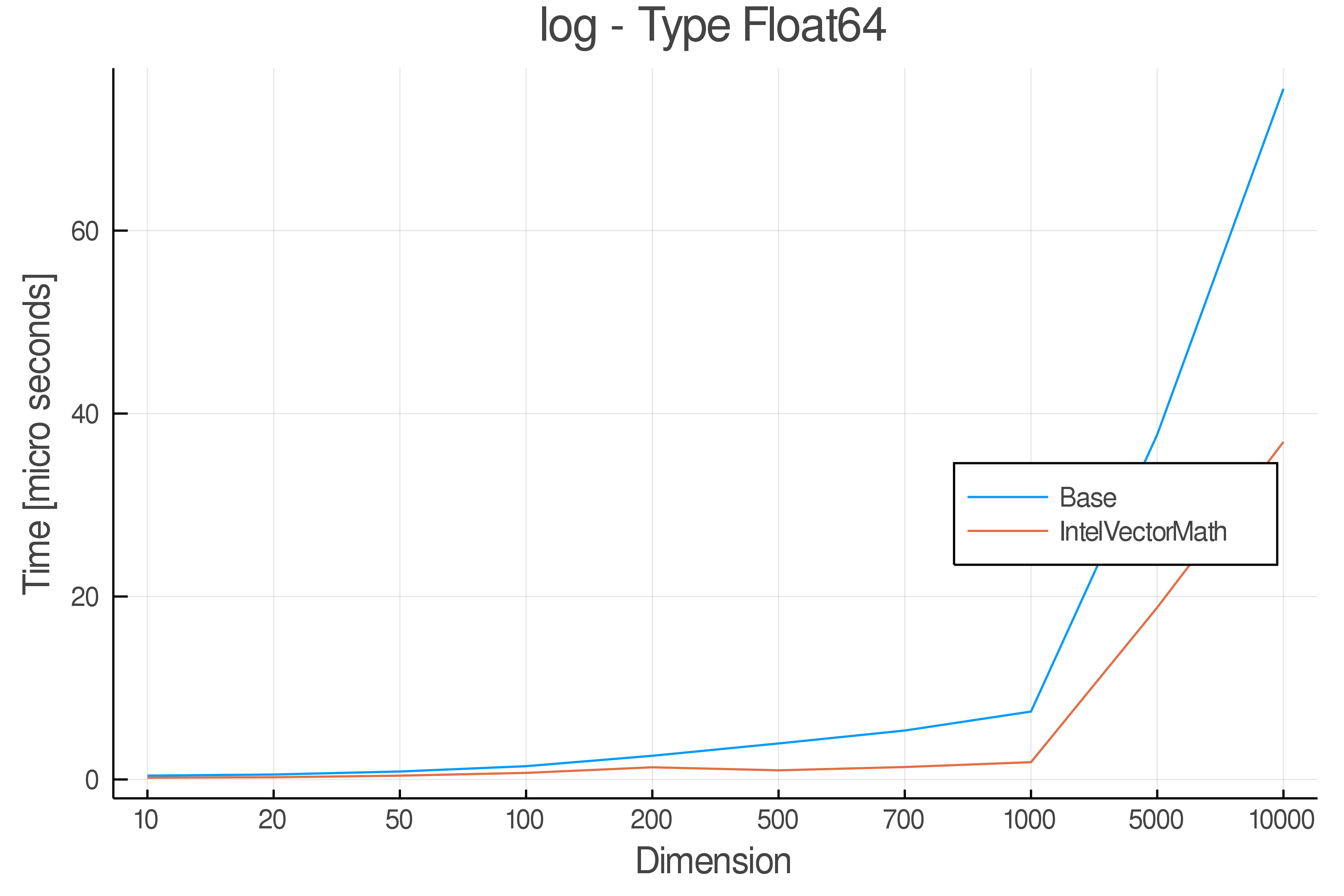
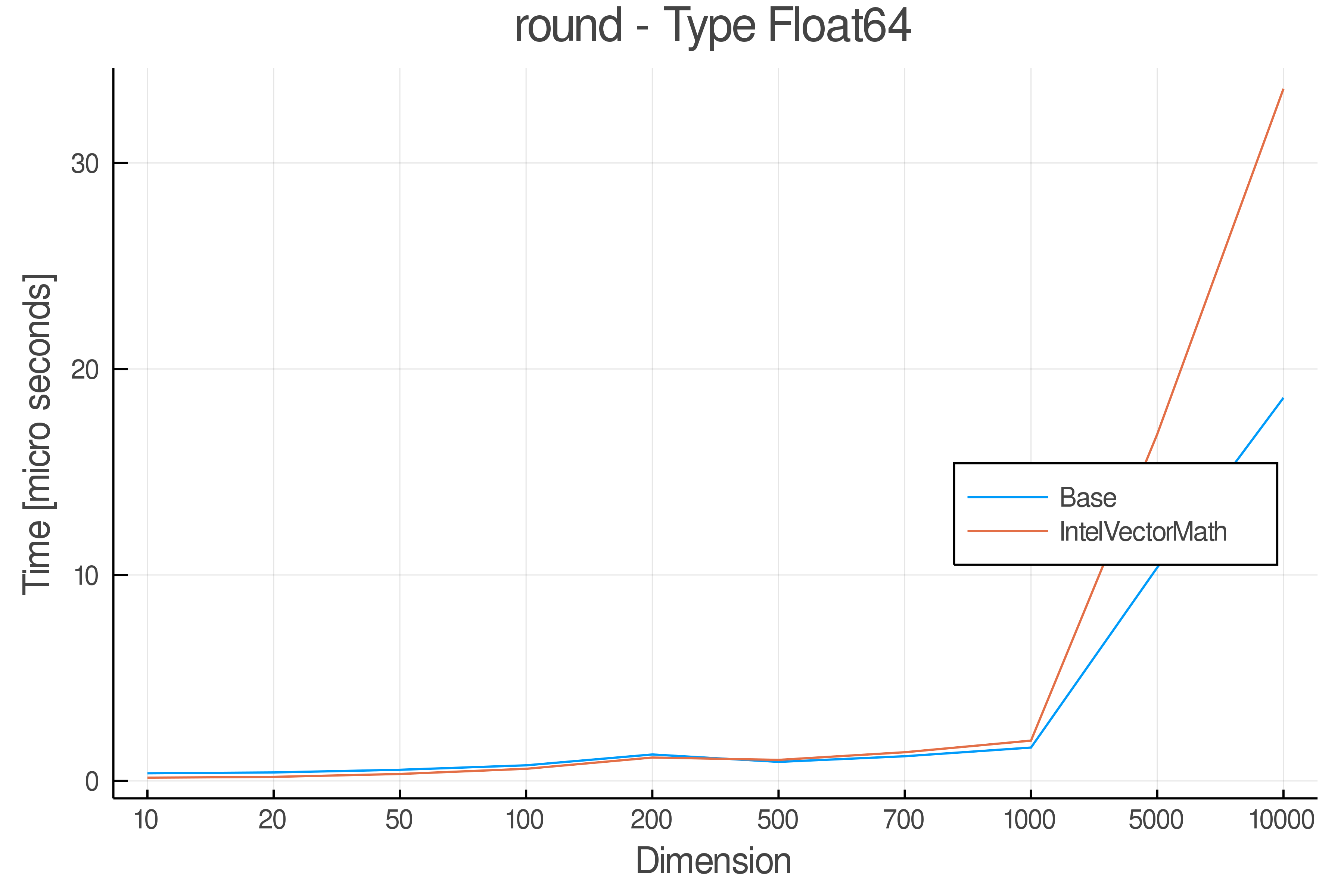
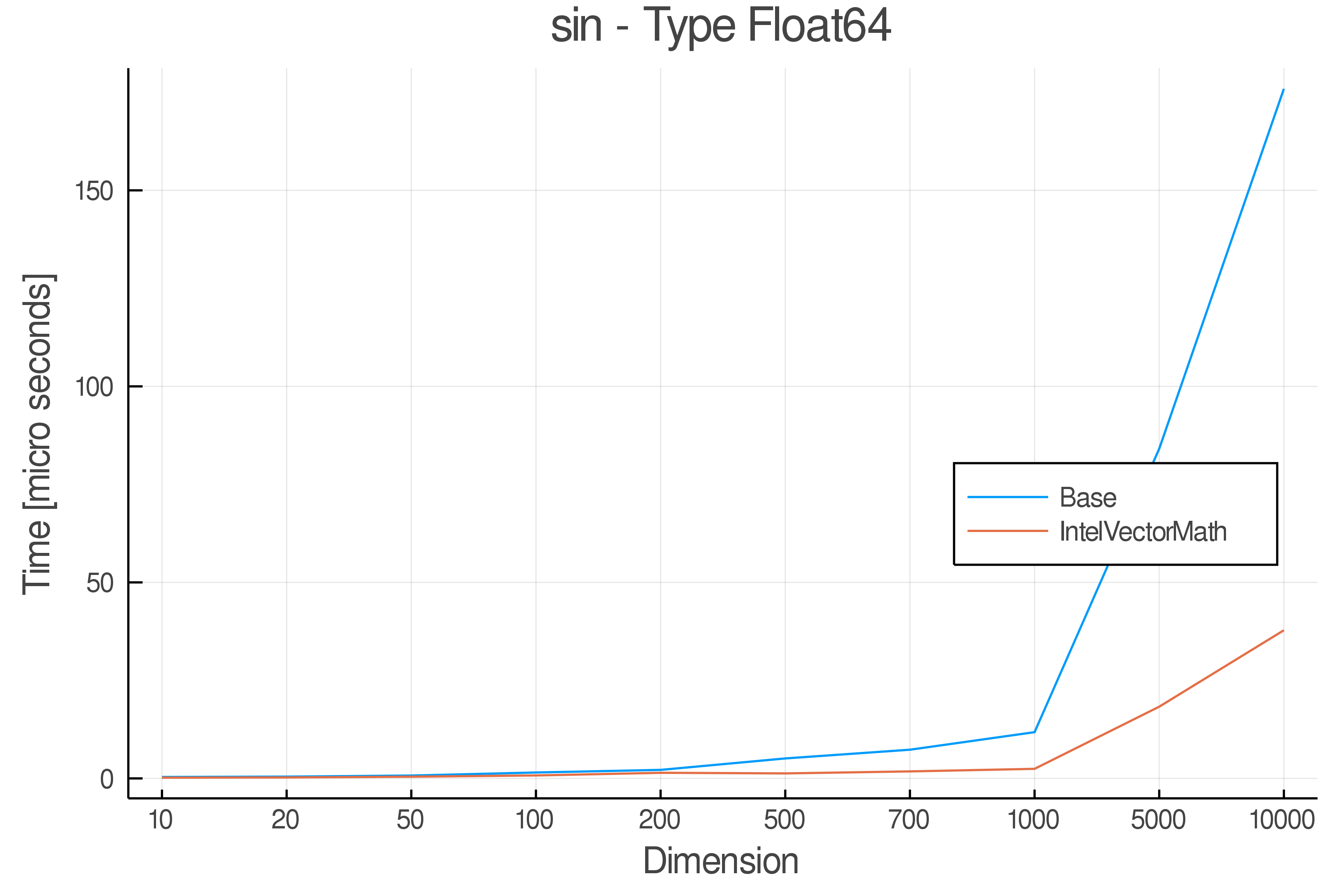
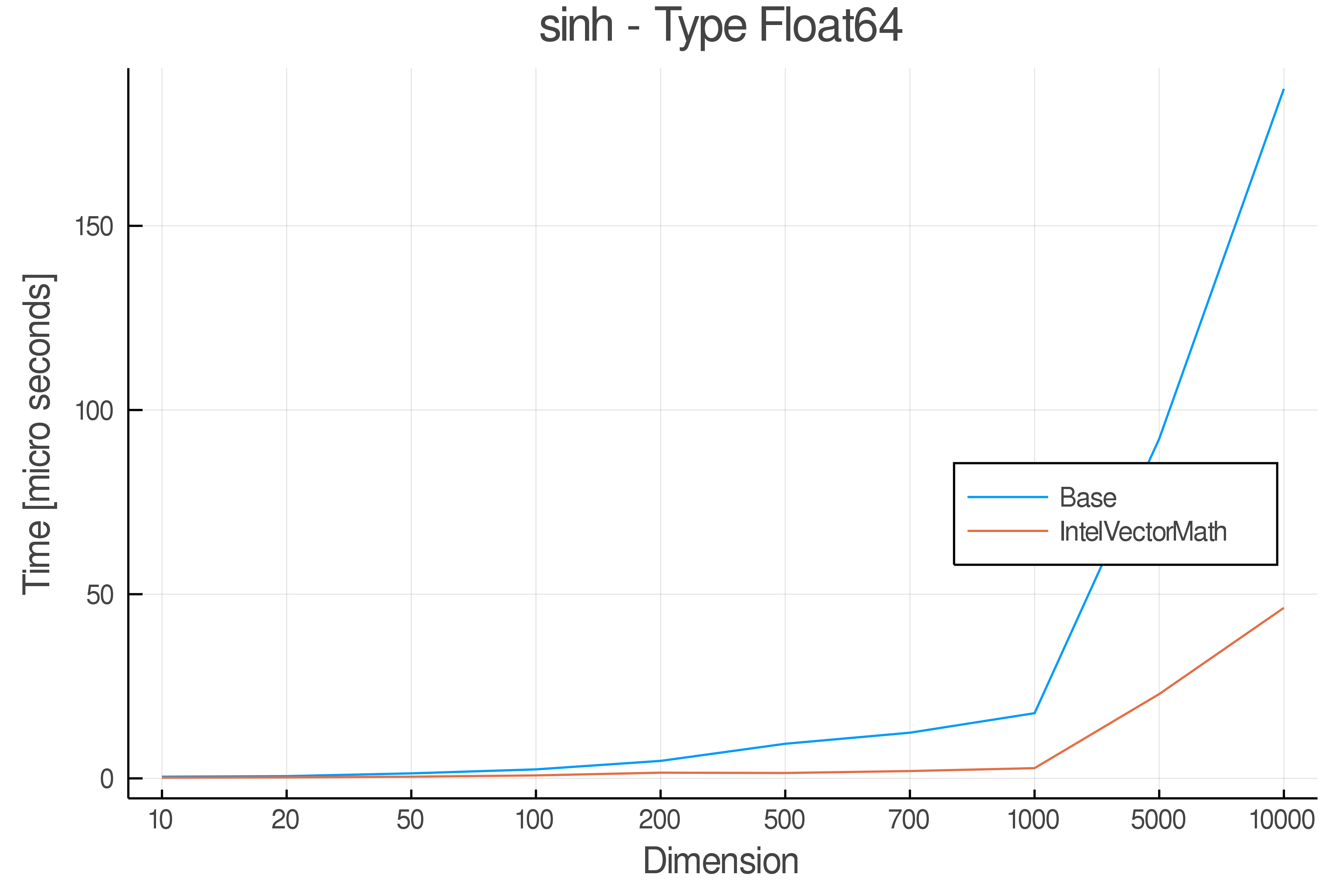
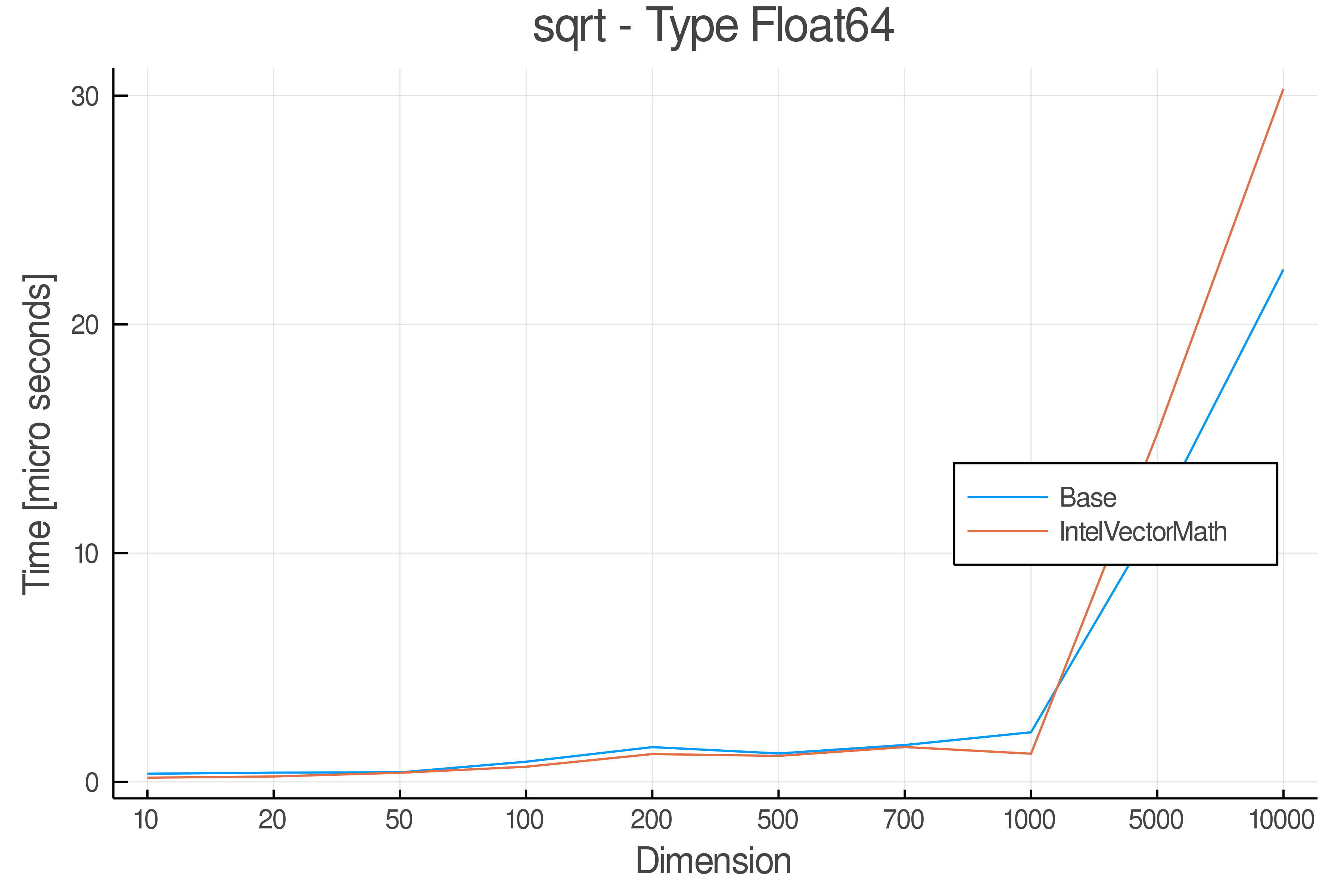
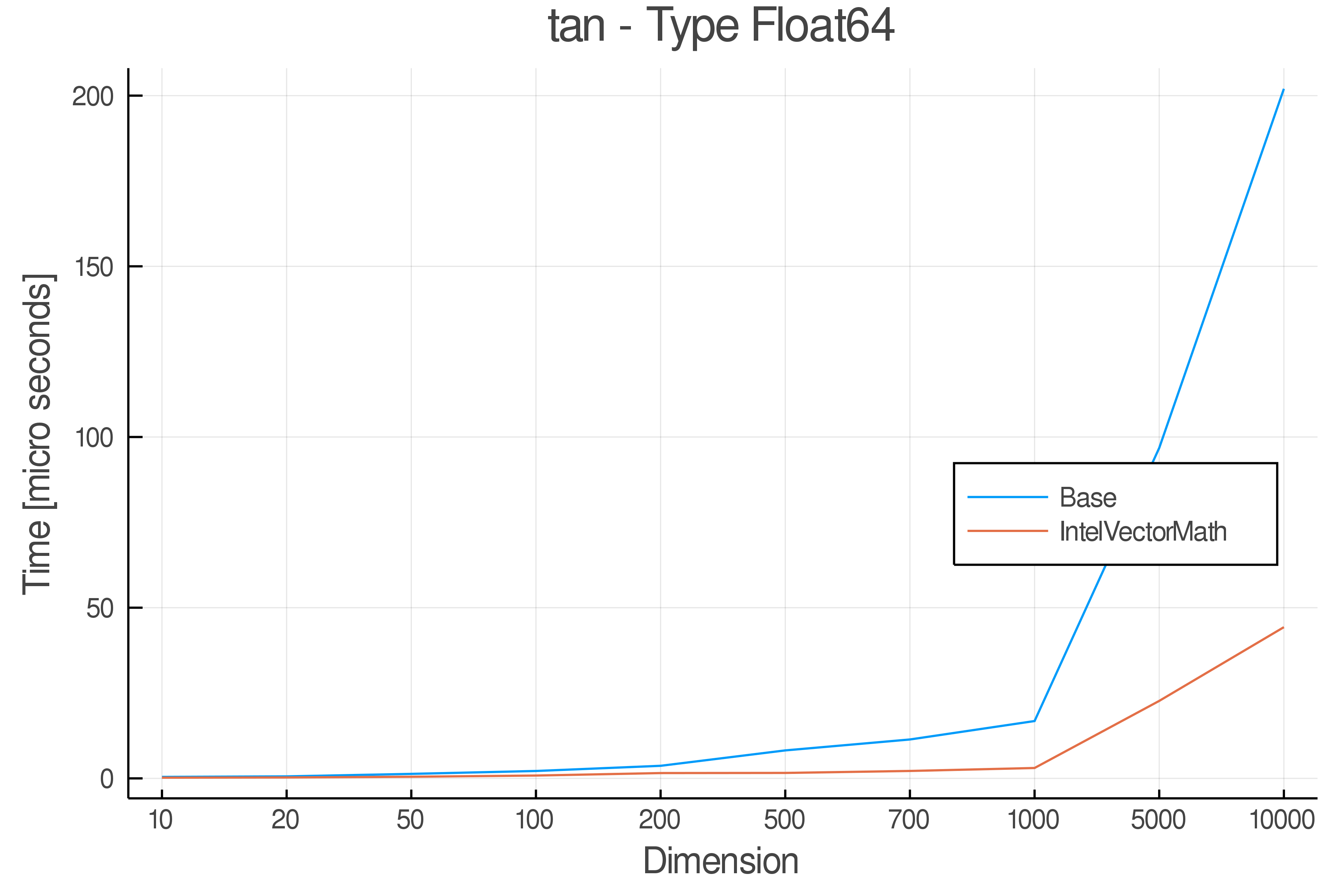
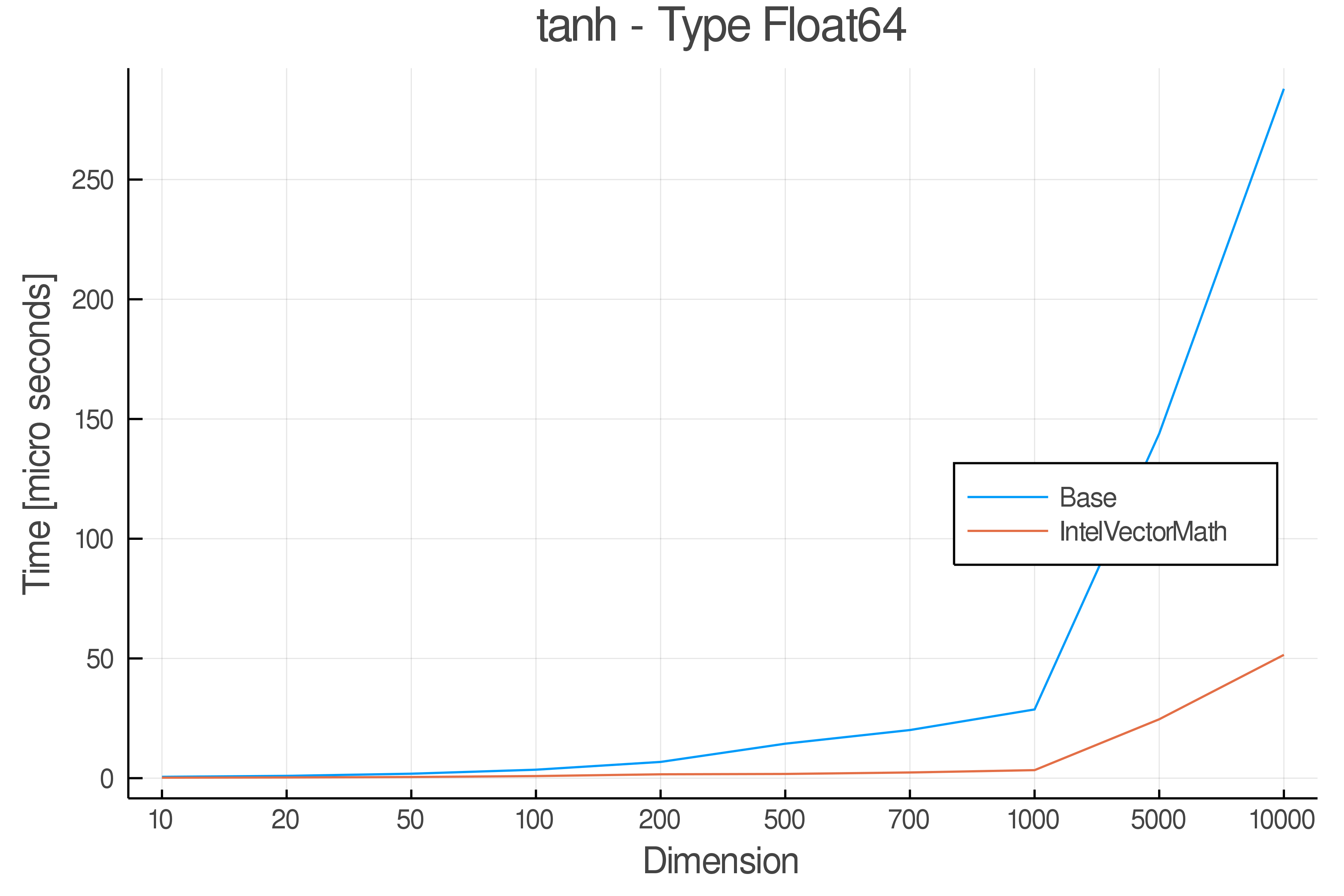
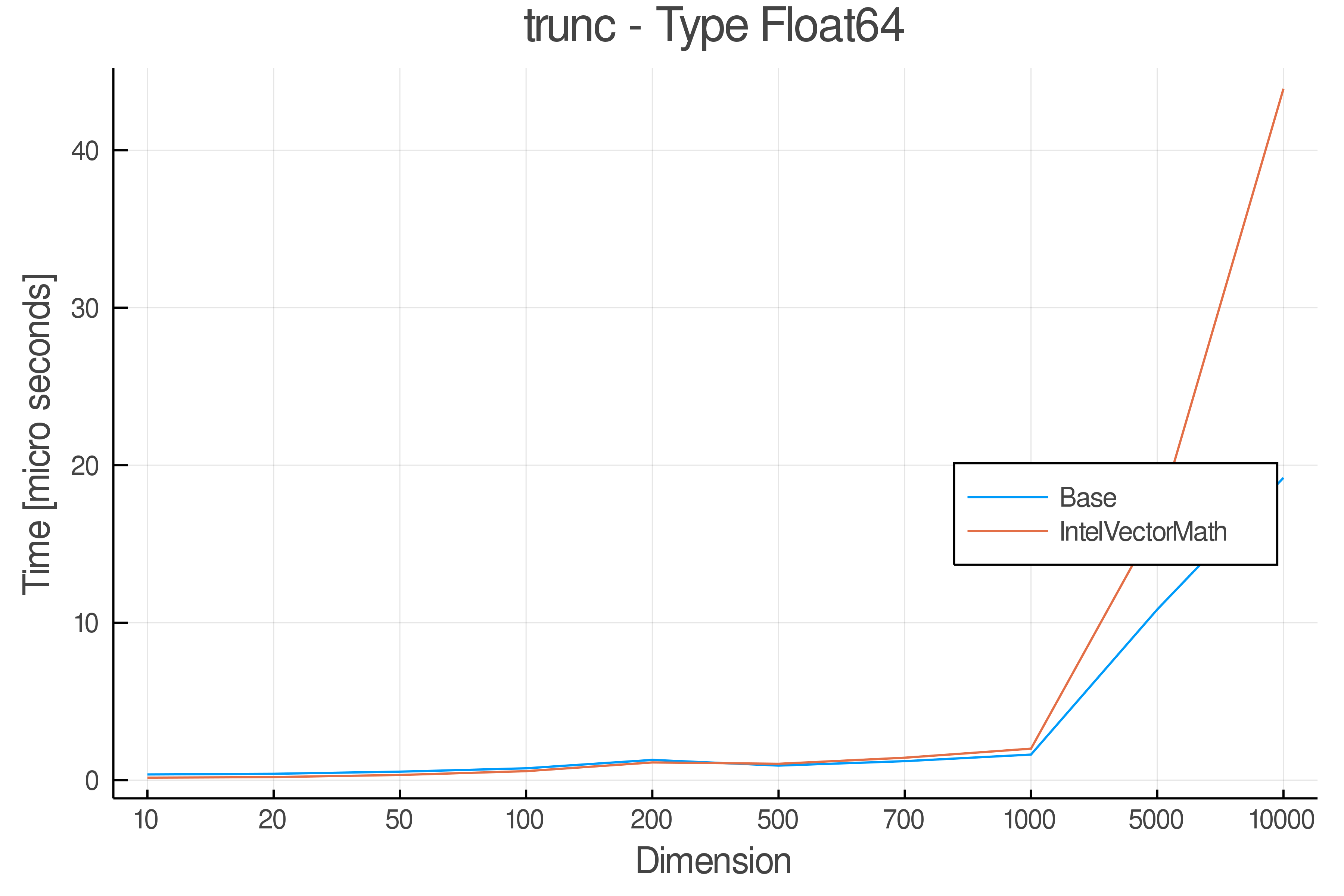
+ Real Functions - Performance over dimensions
+
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
+
+
+
+
+
+Tests were performed on an Intel(R) Core(TM) i5-8250U @ 1.6 [GHz] 1800 Mhz. The dashed line indicates equivalent performance for IntelVectorMath versus the implementations in Base.
## Supported functions
diff --git a/benchmark-results b/benchmark-results
new file mode 160000
index 0000000..06b87cb
--- /dev/null
+++ b/benchmark-results
@@ -0,0 +1 @@
+Subproject commit 06b87cb1af133afb00b16a237c18a0036aa1fe42
diff --git a/benchmark/Project.toml b/benchmark/Project.toml
new file mode 100644
index 0000000..9a04eff
--- /dev/null
+++ b/benchmark/Project.toml
@@ -0,0 +1,2 @@
+[deps]
+AcuteBenchmark = "8f64fb4b-d933-4fa5-a855-09390d771cf3"
diff --git a/benchmark/benchmark.jl b/benchmark/benchmark.jl
index c8ffbf1..2c8d5c1 100644
--- a/benchmark/benchmark.jl
+++ b/benchmark/benchmark.jl
@@ -1,150 +1,231 @@
-using IntelVectorMath
-using Distributions, Statistics, BenchmarkTools # for benchmark
-using Plots # for plotting
-using JLD2, FileIO # to save file
+using IntelVectorMath, SpecialFunctions
+using AcuteBenchmark
-cd(dirname(@__FILE__))
-include(joinpath(dirname(dirname(@__FILE__)), "test", "common.jl"))
-
-################################################################
-complex = !isempty(ARGS) && ARGS[1] == "complex"
-complex = false
-
-# First generate some random data and test functions in Base on it
-const NVALS = 10_000
-base_unary = complex ? base_unary_complex : base_unary_real
-base_binary = complex ? base_binary_complex : base_binary_real
-types = complex ? (Complex64, Complex128) : (Float32, Float64)
-
-# arrays of inputs are stored in a Tuple. So later for calling use inp... to get the content of the Tuple
-input = Dict( t =>
-[
- [(randindomain(t, NVALS, domain),) for (_, _, domain) in base_unary];
- [(randindomain(t, NVALS, domain1), randindomain(t, NVALS, domain2)) for (_, _, domain1, domain2) in base_binary];
- # (randindomain(t, NVALS, (0, 100)), randindomain(t, 1, (-1, 20))[1])
-]
- for t in types)
-
-fns = [[x[1:2] for x in base_unary_real];
- [x[1:2] for x in base_binary_real]]
+cd(@__DIR__)
+rootPath = pwd()
################################################################
+# Dimensions
+oneArgDims = [10 20 50 100 200 500 700 1000 5000 10000]
+
+twoArgDims = [10 20 50 100 200 500 700 1000 5000 10000; # arg1
+ 10 20 50 100 200 500 700 1000 5000 10000] # arg2
-"""
- bench(fns, input)
-
-benchmark function for IntelVectorMath.jl. Calls both Base and IntelVectorMath functions and stores the benchmarks in two nested Dict. First layer specifies type, and second layer specifies the function name. The result is a Tuple, 1st element being benchmark for Base/SpecialFunctions and 2nd element being for IntelVectorMath.
-
-# Examples
-```julia
-fns = [(:Base, :acos); (:Base, :atan); (:SpecialFunctions, :ref)] # array of tuples
-input = Dict( Float64 => [(rand(1000)); (rand(1000), rand(1000)); (rand(1000))]) # Dict of array of tuples
-times = bench(fns, input)
-
-times[Float64][:acos][1] # Base.acos benchmark for Float64
-times[Float64][:acos][2] # IntelVectorMath.acos benchmark for Float64
-```
-"""
-function bench(fns, input)
- Dict(t => begin
- Dict( fn[2] => begin
- base_fn = eval(:($(fn[1]).$(fn[2])))
- vml_fn = eval(:(IntelVectorMath.$(fn[2])))
- println("benchmarking $vml_fn for type $t")
- timesBase = @benchmark $base_fn.($inp...)
- timesVML = @benchmark $vml_fn($inp...)
-
- [timesBase, timesVML]
- end for (fn, inp) in zip(fns, input[t]) )
- end for t in types)
-end
################################################################
+## Real Functions
+
+typesReal=[Float32, Float64]
+
+configsRealBase = FunbArray([
+
+ # oneArgDims
+ Funb(acos, [(-1, 1)], typesReal, oneArgDims),
+ Funb(asin, [(-1, 1)], typesReal, oneArgDims),
+ Funb(atan, [(-50, 50)], typesReal, oneArgDims),
+ Funb(cos, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(sin, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(tan, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(acosh, [(1, 1000)], typesReal, oneArgDims),
+ Funb(asinh, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(atanh, [(-1, 1)], typesReal, oneArgDims),
+ Funb(cosh, [(0, 89.415985f0)], typesReal, oneArgDims),
+ Funb(sinh, [(-89.415985f0, 89.415985f0)], typesReal, oneArgDims),
+ Funb(tanh, [(-8.66434f0, 8.66434f0)], typesReal, oneArgDims),
+ Funb(cbrt, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(sqrt, [(0, 1000)], typesReal, oneArgDims),
+ Funb(exp, [(-88.72284f0, 88.72284f0)], typesReal, oneArgDims),
+ Funb(expm1, [(-88.72284f0, 88.72284f0)], typesReal, oneArgDims),
+ Funb(log, [(0, 1000)], typesReal, oneArgDims),
+ # Funb(log10, [(0, 1000)], typesReal, oneArgDims), # faulty
+ Funb(abs, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(abs2, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(ceil, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(floor, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(round, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(trunc, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(cis, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(SpecialFunctions.erf, [(-3.8325067f0, 3.8325067f0)], typesReal, oneArgDims),
+ Funb(SpecialFunctions.erfc, [(-3.7439213f0, 10.019834f0)], typesReal, oneArgDims),
+ Funb(SpecialFunctions.erfinv, [(-1, 1)], typesReal, oneArgDims),
+ Funb(SpecialFunctions.erfcinv, [(0, 2)], typesReal, oneArgDims),
+ # Funb(SpecialFunctions.lgamma, [(0, 1000)], typesReal, oneArgDims),
+ Funb(SpecialFunctions.gamma, [(0, 36)], typesReal, oneArgDims),
+
+ # twoArgDims
+ Funb(atan, [(-1, 1), (-1, 1)], typesReal, twoArgDims),
+ Funb(hypot, [(-1000, 1000), (-1000, 1000)], typesReal, twoArgDims),
+ # Funb(/, [(-1000, 1000), (-1000, 1000)], typesReal, twoArgDims),
+ # Funb(^, [(0, 100), (-5, 20)], typesReal, twoArgDims),
+])
+
+configsRealIVM = FunbArray([
+
+ # oneArgDims
+ Funb(IVM.acos, [(-1, 1)], typesReal, oneArgDims),
+ Funb(IVM.asin, [(-1, 1)], typesReal, oneArgDims),
+ Funb(IVM.atan, [(-50, 50)], typesReal, oneArgDims),
+ Funb(IVM.cos, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.sin, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.tan, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.acosh, [(1, 1000)], typesReal, oneArgDims),
+ Funb(IVM.asinh, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.atanh, [(-1, 1)], typesReal, oneArgDims),
+ Funb(IVM.cosh, [(0, 89.415985f0)], typesReal, oneArgDims),
+ Funb(IVM.sinh, [(-89.415985f0, 89.415985f0)], typesReal, oneArgDims),
+ Funb(IVM.tanh, [(-8.66434f0, 8.66434f0)], typesReal, oneArgDims),
+ Funb(IVM.cbrt, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.sqrt, [(0, 1000)], typesReal, oneArgDims),
+ Funb(IVM.exp, [(-88.72284f0, 88.72284f0)], typesReal, oneArgDims),
+ Funb(IVM.expm1, [(-88.72284f0, 88.72284f0)], typesReal, oneArgDims),
+ Funb(IVM.log, [(0, 1000)], typesReal, oneArgDims),
+ # Funb(IVM.log10, [(0, 1000)], typesReal, oneArgDims), # faulty
+ Funb(IVM.abs, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.abs2, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.ceil, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.floor, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.round, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.trunc, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.cis, [(-1000, 1000)], typesReal, oneArgDims),
+ Funb(IVM.erf, [(-3.8325067f0, 3.8325067f0)], typesReal, oneArgDims),
+ Funb(IVM.erfc, [(-3.7439213f0, 10.019834f0)], typesReal, oneArgDims),
+ Funb(IVM.erfinv, [(-1, 1)], typesReal, oneArgDims),
+ Funb(IVM.erfcinv, [(0, 2)], typesReal, oneArgDims),
+ # Funb(IVM.lgamma, [(0, 1000)], typesReal, oneArgDims), # faulty
+ Funb(IVM.gamma, [(0, 36)], typesReal, oneArgDims),
+
+ # twoArgDims
+ Funb(IVM.atan, [(-1, 1), (-1, 1)], typesReal, twoArgDims),
+ Funb(IVM.hypot, [(-1000, 1000), (-1000, 1000)], typesReal, twoArgDims),
+ # Funb(IVM.(/), [(-1000, 1000), (-1000, 1000)], typesReal, twoArgDims),
+ # Funb(IVM.(^), [(0, 100), (-5, 20)], typesReal, twoArgDims),
+])
-# do benchmark
-benches = bench(fns, input)
+################################################################
+# Complex Functions
+
+typesComplex=[Complex{Float32}, Complex{Float64}]
+
+configsComplexBase = FunbArray([
+ # oneArgDims
+ Funb(acos, [(-1, 1)], typesComplex, oneArgDims),
+ Funb(asin, [(-1, 1)], typesComplex, oneArgDims),
+ # Funb(atan, [(-50, 50)], typesComplex, oneArgDims),
+ # Funb(cos, [(-10, 10)], typesComplex, oneArgDims),
+ # Funb(sin, [(-10, 10)], typesComplex, oneArgDims),
+ # Funb(tan, [(-10, 10)], typesComplex, oneArgDims),
+ Funb(acosh, [(1, 1000)], typesComplex, oneArgDims),
+ Funb(asinh, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(atanh, [(-1, 1)], typesComplex, oneArgDims),
+ # Funb(cosh, [(0, 89.415985f0)], typesComplex, oneArgDims),
+ # Funb(sinh, [(-89.415985f0, 89.415985f0)], typesComplex, oneArgDims),
+ # Funb(tanh, [(-8.66434f0, 8.66434f0)], typesComplex, oneArgDims),
+ Funb(sqrt, [(0, 1000)], typesComplex, oneArgDims),
+ Funb(exp, [(-88.72284f0, 88.72284f0)], typesComplex, oneArgDims),
+ Funb(log, [(0, 1000)], typesComplex, oneArgDims),
+ # Funb(log10, [(0, 1000)], typesComplex, oneArgDims),
+ Funb(abs, [(-1000, 1000)], typesComplex, oneArgDims),
+ Funb(angle, [(-1000, 1000)], typesComplex, oneArgDims),
+ Funb(conj, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(cis, [(-1000, 1000)], typesComplex, oneArgDims),
+
+ # twoArgDims
+ # Funb(/, [(-1000, 1000), (-1000, 1000)], typesComplex, twoArgDims),
+ # Funb(^, [(0, 100), (-2, 10)], typesComplex, twoArgDims),
+
+ # missing?
+ ## oneArgDims
+
+ # Funb(cbrt, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(expm1, [(-88.72284f0, 88.72284f0)], typesComplex, oneArgDims),
+ # Funb(abs2, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(ceil, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(SpecialFunctions.erf, [(-3.8325067f0, 3.8325067f0)], typesComplex, oneArgDims),
+ # Funb(SpecialFunctions.erfc, [(-3.7439213f0, 10.019834f0)], typesComplex, oneArgDims),
+ # Funb(SpecialFunctions.erfinv, [(-1, 1)], typesComplex, oneArgDims),
+ # Funb(SpecialFunctions.erfcinv, [(0, 2)], typesComplex, oneArgDims),
+ # Funb(SpecialFunctions.lgamma, [(0, 1000)], typesComplex, oneArgDims),
+ # Funb(SpecialFunctions.gamma, [(0, 36)], typesComplex, oneArgDims),
+ # Funb(floor, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(round, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(trunc, [(-1000, 1000)], typesComplex, oneArgDims),
+
+ ## twoArgDims
+ # Funb(atan, [(-1, 1), (-1, 1)], typesComplex, twoArgDims),
+ # Funb(hypot, [(-1000, 1000), (-1000, 1000)], typesComplex, twoArgDims),
+])
+
+configsComplexIVM = FunbArray([
+ # oneArgDims
+ Funb(IVM.acos, [(-1, 1)], typesComplex, oneArgDims),
+ Funb(IVM.asin, [(-1, 1)], typesComplex, oneArgDims),
+ # Funb(IVM.atan, [(-50, 50)], typesComplex, oneArgDims),
+ # Funb(IVM.cos, [(-10, 10)], typesComplex, oneArgDims),
+ # Funb(IVM.sin, [(-10, 10)], typesComplex, oneArgDims),
+ # Funb(IVM.tan, [(-10, 10)], typesComplex, oneArgDims),
+ Funb(IVM.acosh, [(1, 1000)], typesComplex, oneArgDims),
+ Funb(IVM.asinh, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.atanh, [(-1, 1)], typesComplex, oneArgDims),
+ # Funb(IVM.cosh, [(0, 89.415985f0)], typesComplex, oneArgDims),
+ # Funb(IVM.sinh, [(-89.415985f0, 89.415985f0)], typesComplex, oneArgDims),
+ # Funb(IVM.tanh, [(-8.66434f0, 8.66434f0)], typesComplex, oneArgDims),
+ Funb(IVM.sqrt, [(0, 1000)], typesComplex, oneArgDims),
+ Funb(IVM.exp, [(-88.72284f0, 88.72284f0)], typesComplex, oneArgDims),
+ Funb(IVM.log, [(0, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.log10, [(0, 1000)], typesComplex, oneArgDims),
+ Funb(IVM.abs, [(-1000, 1000)], typesComplex, oneArgDims),
+ Funb(IVM.angle, [(-1000, 1000)], typesComplex, oneArgDims),
+ Funb(IVM.conj, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.cis, [(-1000, 1000)], typesComplex, oneArgDims),
+
+ # twoArgDims
+ # Funb(IVM.(/), [(-1000, 1000), (-1000, 1000)], typesComplex, twoArgDims),
+ # Funb(IVM.(^), [(0, 100), (-2, 10)], typesComplex, twoArgDims),
+
+ # missing?
+ ## oneArgDims
+
+ # Funb(IVM.cbrt, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.expm1, [(-88.72284f0, 88.72284f0)], typesComplex, oneArgDims),
+ # Funb(IVM.abs2, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.ceil, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.erf, [(-3.8325067f0, 3.8325067f0)], typesComplex, oneArgDims),
+ # Funb(IVM.erfc, [(-3.7439213f0, 10.019834f0)], typesComplex, oneArgDims),
+ # Funb(IVM.erfinv, [(-1, 1)], typesComplex, oneArgDims),
+ # Funb(IVM.erfcinv, [(0, 2)], typesComplex, oneArgDims),
+ # Funb(IVM.lgamma, [(0, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.gamma, [(0, 36)], typesComplex, oneArgDims),
+ # Funb(IVM.floor, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.round, [(-1000, 1000)], typesComplex, oneArgDims),
+ # Funb(IVM.trunc, [(-1000, 1000)], typesComplex, oneArgDims),
+
+ ## twoArgDims
+ # Funb(IVM.atan, [(-1, 1), (-1, 1)], typesComplex, twoArgDims),
+ # Funb(IVM.hypot, [(-1000, 1000), (-1000, 1000)], typesComplex, twoArgDims),
+])
-@save "benchmarkData.jld" benches
-# @save "benchmarkData-complex.jld" benches
+################################################################
+# Performing Benchmarks
+# Real
+println("\nBenchmarking Base Real Functions\n")
+benchmark!(configsRealBase)
-# benches = load("benchmarkData.jld2", "benches")
+println("\nBenchmarking IntelVectorMath Real Functions\n")
+benchmark!(configsRealIVM)
+cd(joinpath(rootPath,"Real"))
-# something is wrong with these
-deleteat!(fns, [18, 31])
-delete!(benches[Float32], :lgamma)
-delete!(benches[Float64], :lgamma)
-delete!(benches[Float32], :log10)
-delete!(benches[Float64], :log10)
+bar(configsRealBase => configsRealIVM, uniqueType = true, dimAnnotation = false, uniqueDim = true, configName = "Base" => "IntelVectorMath")
+dimplot([configsRealBase,configsRealIVM],["Base", "IntelVectorMath"])
################################################################
+# Complex
+println("\nBenchmarking Base Complex Functions\n")
+benchmark!(configsComplexBase)
-"""
-benchmark analysis function
-"""
-function ratioci(y, x, alpha = 0.05)
- tq² = abs2(quantile(TDist(length(x) + length(y) - 2), alpha))
- μx = mean(x)
- σx² = varm(x, μx)
- μy = mean(y)
- σy² = varm(y, μy)
- a = sqrt((μx * μy)^2 - (μx^2 - tq² * σx²) * (μy^2 - tq² * σy²))
- b = μx^2 - tq² * σx²
- return (((μx * μy) - a) / b, ((μx * μy) + a) / b)
-end
-
-################################################################
+println("\nBenchmarking IntelVectorMath Complex Functions\n")
+benchmark!(configsComplexIVM)
-"""
-Does analysis of the benchmark data and plots them as bars.
-"""
-function plotBench()
-
-# Print ratio
- colors = [:blue, :red]
- for itype = 1:length(types)
-
- # creating arrays of times from benchmarks
- benchVals = collect(values(benches[types[itype]]))
- builtint = [x[1].times for x in benchVals]
- vmlt = [x[2].times for x in benchVals]
-
- # calculating mean of run times
- μ = vec(map(mean, builtint) ./ map(mean, vmlt))
-
- # error bar disabled because benchmark tools takes care of errors
-
- # # calculating error bars
- # ci = zeros(Float64, 2, length(fns))
- # for ifn = 1:length(builtint)
- # lower, upper = ratioci(builtint[ifn], vmlt[ifn])
- # ci[1, ifn] = μ[ifn] - lower
- # ci[2, ifn] = upper - μ[ifn]
- # end
-
- # adding bar
- plt = bar!(
- 0.2+(0.4*itype):length(fns),
- μ,
- # yerror = ci,
- fillcolor = colors[itype],
- labels = [string(x) for x in types],
- dpi = 600
- )
- end
- fname = [string(fn[2]) for fn in fns]
- # if !complex
- # fname[end-1] = "A.^B"
- # fname[end] = "A.^b"
- # end
- xlims!(0, length(fns) + 1)
- xticks!(1:length(fns)+1, fname, rotation = 70, fontsize = 10)
- title!("IntelVectorMath Performance for array of size $NVALS")
- ylabel!("Relative Speed (IntelVectorMath/Base)")
- hline!([1], line=(4, :dash, 0.6, [:green]), labels = 1)
- savefig("performance$(complex ? "_complex" : "").png")
-
-end
+cd(joinpath(rootPath,"Complex"))
-################################################################
+bar(configsComplexBase => configsComplexIVM, uniqueType = true, dimAnnotation = false, uniqueDim = true, configName = "Base" => "IntelVectorMath")
-# do plotting
-plotBench()
+dimplot([configsComplexBase,configsComplexIVM],["Base", "IntelVectorMath"])
diff --git a/benchmark/performance.png b/benchmark/performance.png
deleted file mode 100644
index 12985d6..0000000
Binary files a/benchmark/performance.png and /dev/null differ
diff --git a/benchmark/performance_complex.png b/benchmark/performance_complex.png
deleted file mode 100644
index 3f7c948..0000000
Binary files a/benchmark/performance_complex.png and /dev/null differ